✍️ 朱邓达  •  📅 2025-12-05

如何解决“波形在漂移”的问题？

问题描述

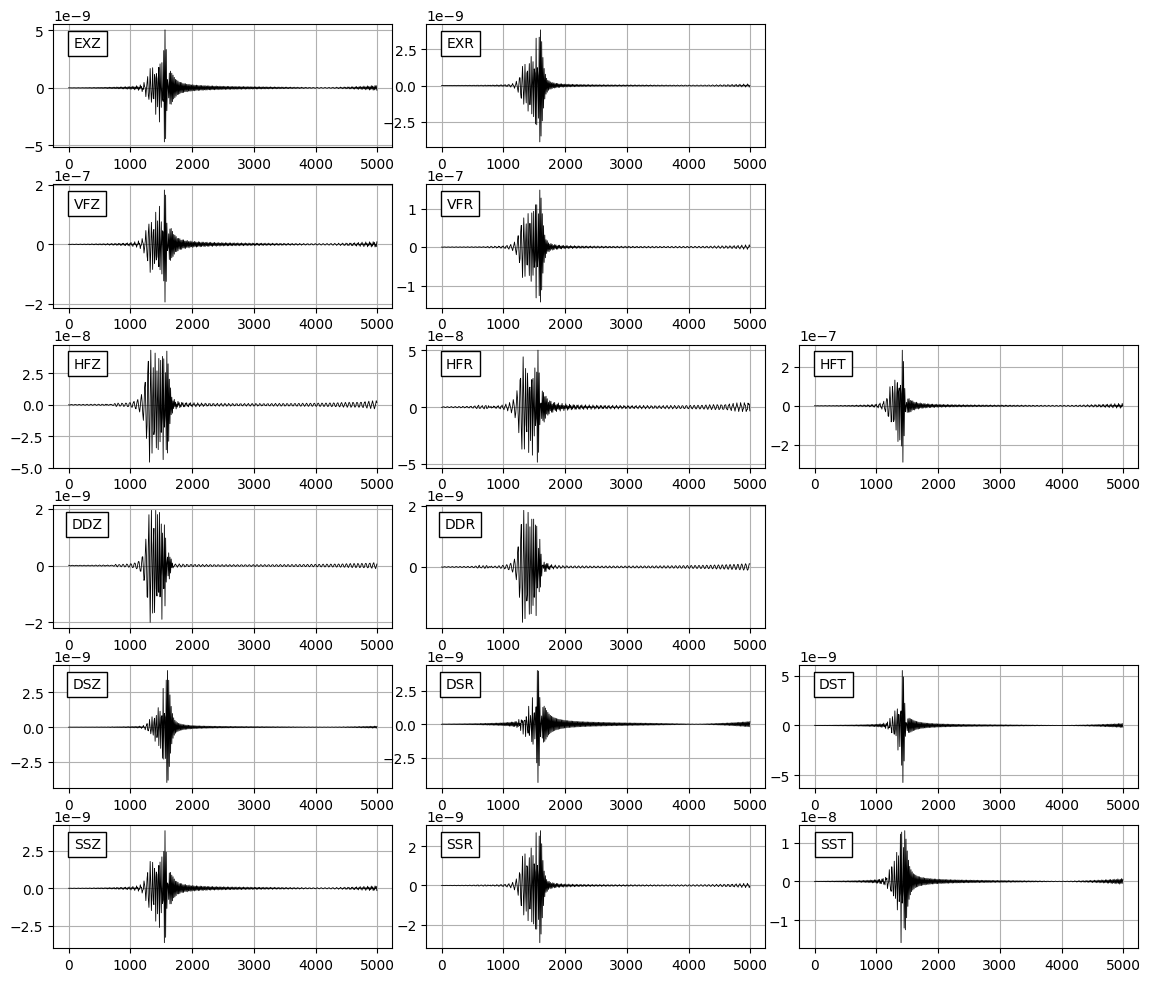
如下所示，以 MILROW 模型为例， 计算震源深度为 10 km，台站在地表，震中距为 5000 km 的格林函数， 采样点数 500，采样间隔 10 秒。仅使用传统的离散波数积分，不使用其他技巧。

脚本下载：run.py

MILROW 模型定义如下，与文档中其它部分一致，

0.2  3.4  1.7  2.3
0.6  3.7  1.9  2.4
0.5  4.2  2.1  2.4
0.5  4.6  2.3  2.5
0.7  4.9  2.8  2.6
0.5  5.1  2.9  2.7
6.0  5.9  3.3  2.7
28   6.9  4.0  2.8
0.0  8.2  4.7  3.2

使用如下命令计算格林函数，

grt greenfn -Mmilrow -D10/0 -N500/10+a -R5000 -OGRN -S

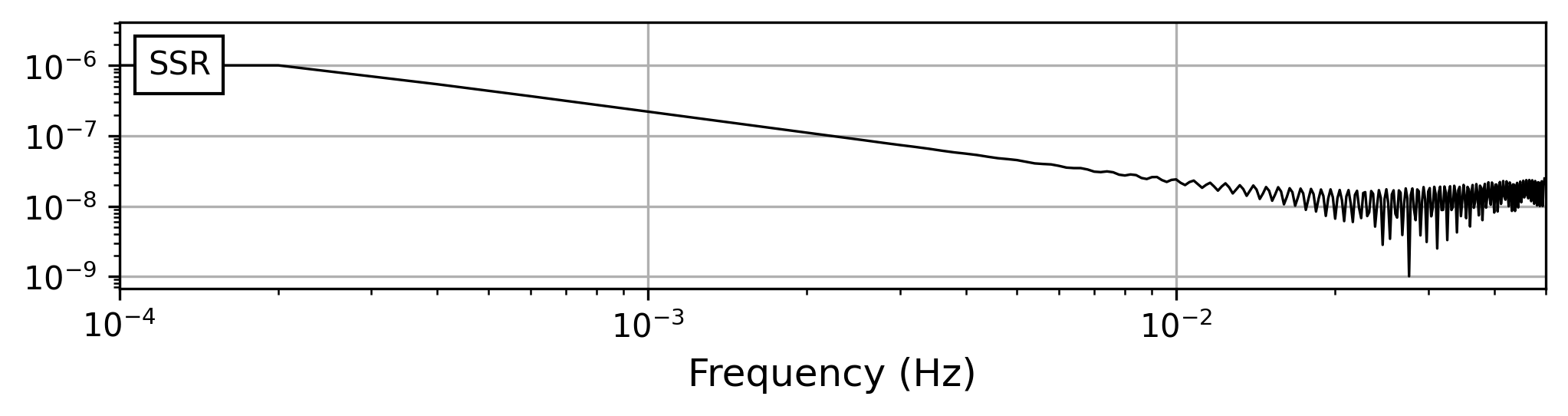
绘制 SSR 波形如下，发现整个波形发生“漂移”。事实上如果绘制所有格林函数会发现它们都发生了不同程度的漂移。

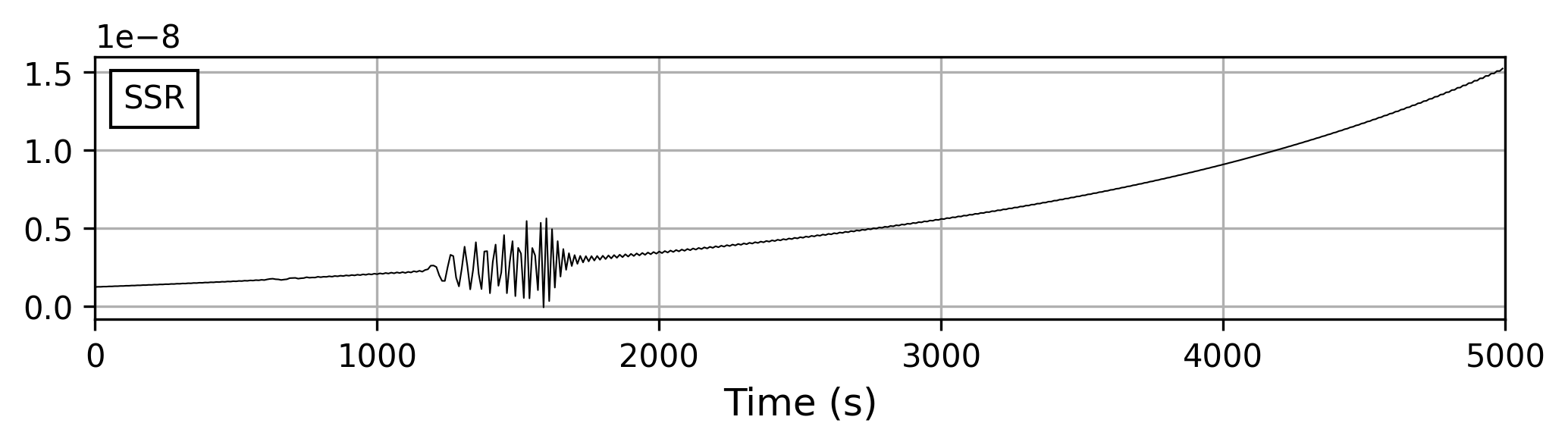
../../_images/grn.png

问题成因

从形态来看，漂移的形态呈 e 指数，很明显是在时域补偿虚频率产生的效果。

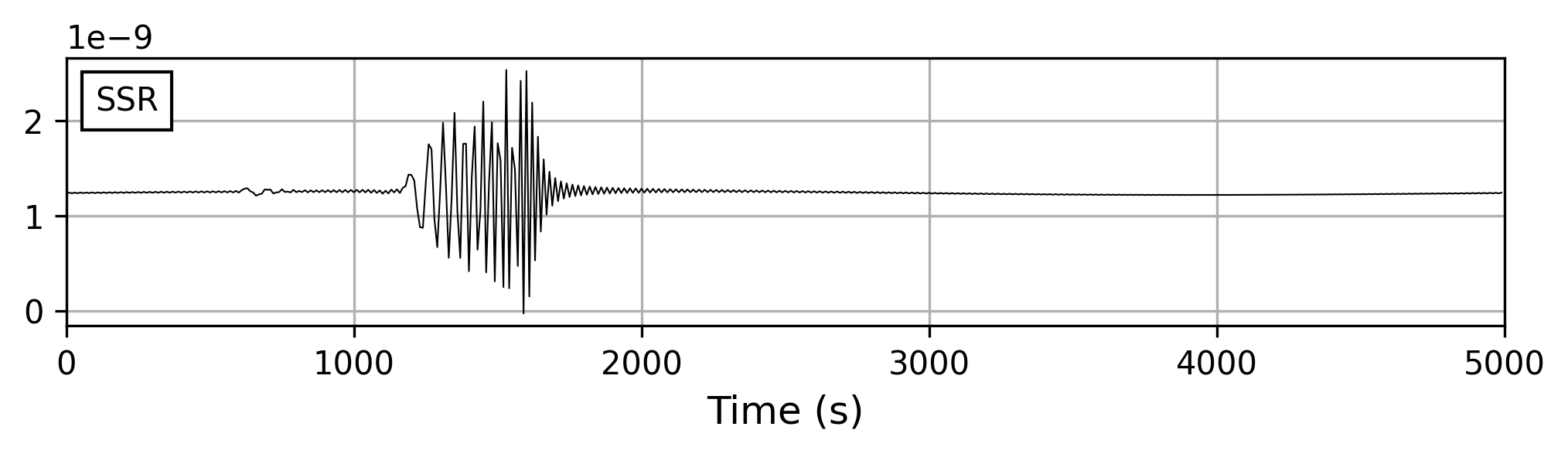
回退虚频率的补偿

我们可以将以上波形再乘以 \(e^{-\omega_I t}\) 以回退虚频率的补偿，观察以下波形形态， 发现整体发生了偏移，即零频结果不准。

../../_images/grn2.png

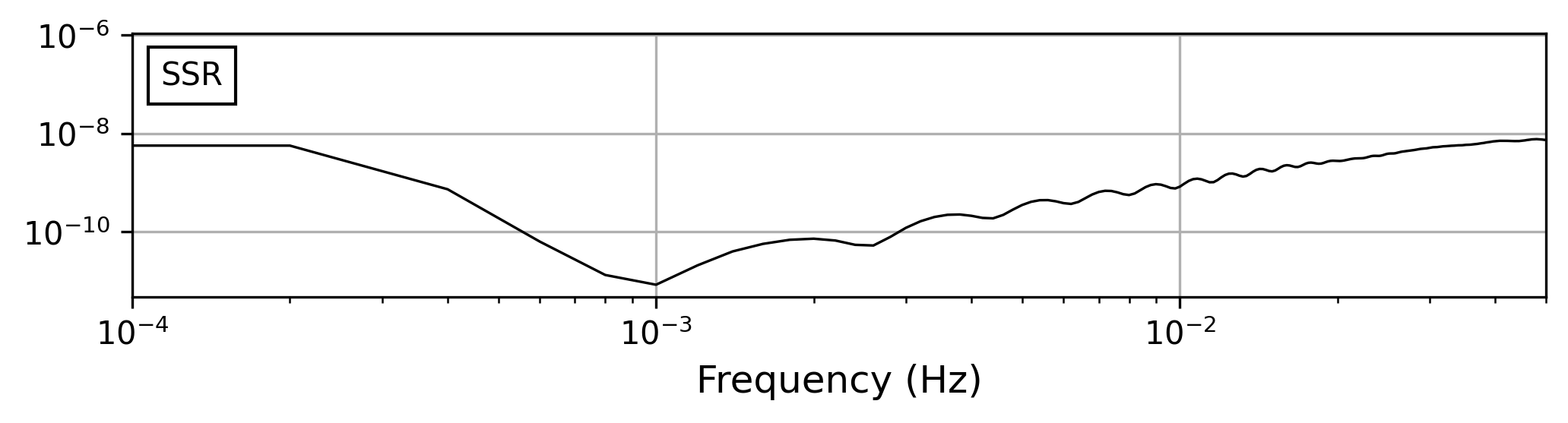
观察频谱

我们再观察频谱， 发现在极低的频段呈现不正常的高值，而虚频率的补偿会进一步放大这一现象， 这表明不止是零频的一个单独问题，而是一系列低频点发生类似问题。

  • 虚频率补偿前

../../_images/grn2_freqs.png

  • 虚频率补偿后

../../_images/grn_freqs.png

观察核函数

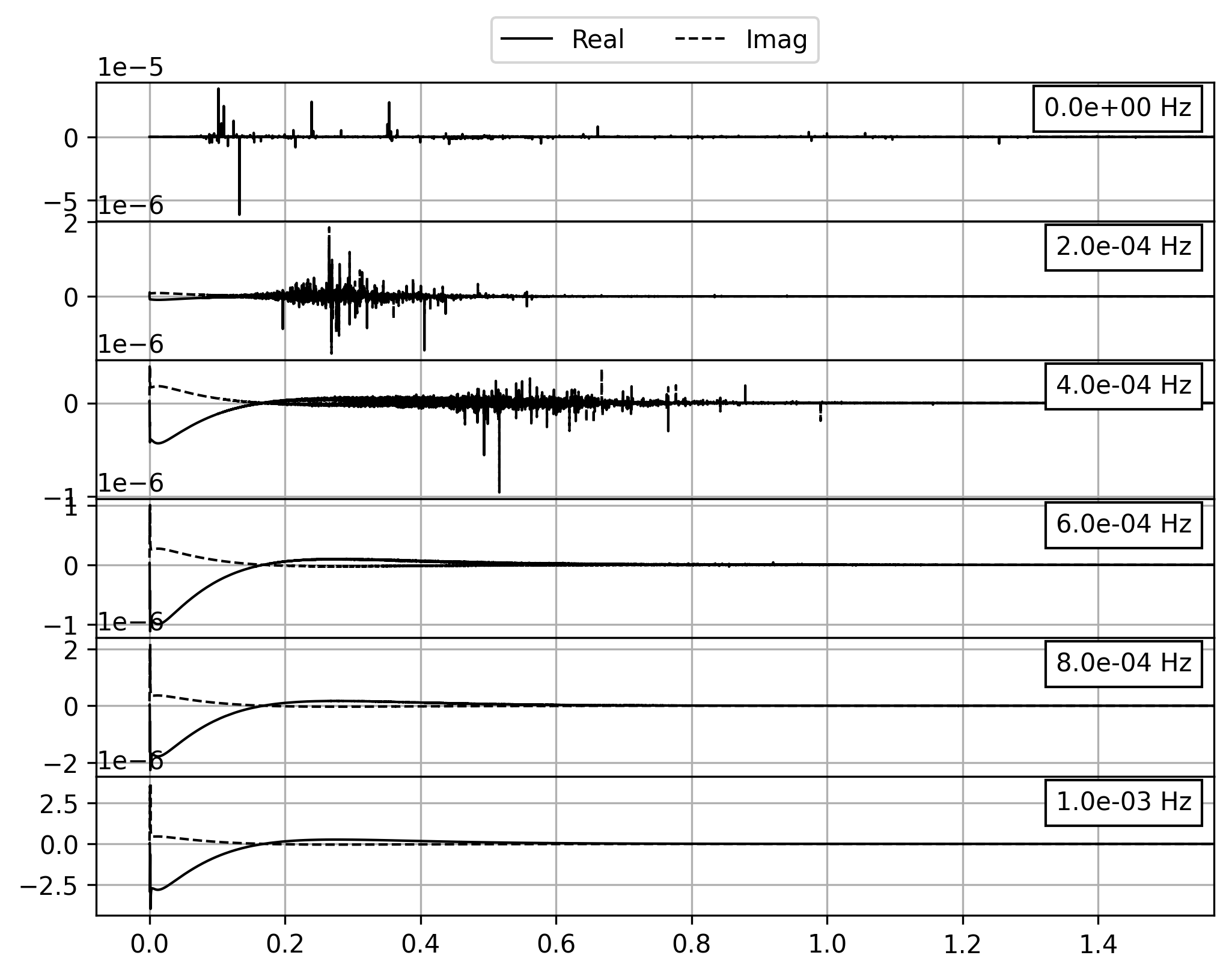
低频段计算发生偏差，显然问题出在核函数。上述在计算格林函数时已经指定了相应的参数以保存核函数。 如下，我们可以绘制几个低频段的核函数，发现核函数曲线存在很多毛刺，这就导致了积分结果发生偏差。

../../_images/kernels.png

虚频率的定义

低频的核函数曲线出现毛刺，这是计算机在做数值计算时发生溢出的表现。 但这个现象在震中距不算太大的情况下并没有出现。事实上，震中距的大小是间接原因， 根本原因是时窗长度。

根据 Bouchon (1981) 的设计，虚频率定义为 \(\omega_I = \zeta \dfrac{\pi}{T}\) ， 其中 \(T\) 为时窗长度。虚频率的加入其中一个目的就是使核函数的极点略微偏离实轴， 从而可以进行常规的波数积分。但当震中距增大，模型速度减小，计算时就需要更宽的时窗来容纳所有有效信号以避免混叠， 代价是虚频率减小，核函数的极点逐渐靠近实轴，导致核函数计算的不稳定性风险增加。

核函数有多个极点，且随频率变化，而从实际计算来看，虚频率的减小对极低频的核函数计算影响很大。 这是因为在核函数的计算中，无时延的广义 R/T 系数矩阵仅和相速度有关，当引入虚频率后，对应的复数形式的相速度定义为 \(\tilde{c}=\dfrac{\omega - j \omega_I}{k}\) ，当实频率 \(\omega\) 和虚频率 \(\omega_I\) 都很小时， \(\tilde{c} \rightarrow 0\) ，这就导致核函数计算不稳定，也就导致低频结果有偏差，整体波形在漂。

解决方法

既然这是方法本身的局限性导致这些低频的几个点计算不出精确结果，不如直接放弃它们。

在以上计算格林函数时，可以看到为了复现上述问题，我添加了一些参数 （ -N+a 和 keepAllFreq ）， 这是因为从 0.13.0 版本起， 程序默认会根据复频率的大小跳过低频的计算。 具体而言，程序不计算 \(|\omega - \omega_I| < 0.1\) 的频谱，并会在终端打印对应的Warning。 这本质就是自动进行了高通滤波。 如果觉得阈值不合适或需要进行数值实验，可加上上述参数以计算所有频率，然后再手动设置频段。

以下是跳过这些频段后的波形（计算时不使用 -N+a 和 keepAllFreq ）。

../../_images/grn3.png