✍️ 朱邓达 • 📅 2025-04-19 • ⚡ 2025-09-22

积分收敛性

通过输出核函数文件，观察源点和场点深度接近时，积分收敛性的变化，以及峰谷平均法的作用。 具体积分表达式以及分类详见 计算动态格林函数。

核函数文件

该文件记录了波数积分过程中不同波数对应的核函数值。以下用法展示了如何输出该文件。

# -S<i1>,<i2>,...表示输出对应频率点索引值的核函数文件
grt greenfn -Mmilrow -D2/0 -N500/0.02 -OGRN -R5,8,10 -S50,100

输出的核函数文件会在 GRN_grtstats/milrow_{depsrc}_{deprcv}/ 路径下。

import numpy as np
import pygrt 

modarr = np.loadtxt("milrow")

depsrc = 2.0
deprcv = 0.0

pymod = pygrt.PyModel1D(modarr, depsrc=depsrc, deprcv=deprcv)

# 通过statsfile参数自定义核函数文件的输出目录, statsidxs指定想输出的频率索引值
distarr = [5,8,10]
stgrnLst = pymod.compute_grn(
    distarr=distarr, nt=500, dt=0.02,
    statsfile=f"pygrtstats_{depsrc}_{deprcv}", statsidxs=[50,100]
)

输出的核函数文件会在自定义路径下。

C和Python导出的核函数文件是一致的，底层调用的是相同的函数。文件名称格式为 K_{iw}_{freq}，其中 {iw} 表示频率索引值， {freq} 表示对应频率(Hz)。文件为自定义的二进制文件， 强烈建议使用Python进行读取及后续处理。这里还是给出两种读取方法。

ker2asc 模块可将单个核函数文件转为文本格式。

grt ker2asc GRN_grtstats/milrow_2_0/K_0050_5.00000e+00 > stats

输出的文件如下，

#                k                              EX_q                              EX_w                              VF_q                              VF_w                              HF_q                              HF_w                              HF_v                              DD_q                              DD_w                              DS_q                              DS_w                              DS_v                              SS_q                              SS_w                              SS_v
18879020e-02   -2.02856187e-01  4.96041014e-01   -1.03425028e+02 -3.18035750e+01   -8.85165377e-02 -9.55284925e-02    4.93158286e+00 -1.21165651e+01   -2.26663577e+01  7.81815163e+00    9.45337168e-02  1.07242144e-01    2.26670306e+01 -7.81854269e+00   -3.25405088e+00  1.97453994e+00   -2.06838177e+02 -6.35936736e+01   -4.60765067e+01 -2.33936178e+02   -1.40769267e+00  8.13116327e-01    4.60781795e+01  2.33944595e+02   -9.49446169e-01  3.27485970e-01    3.95981907e-03  4.49214844e-03    9.49474359e-01 -3.27502350e-01
37758041e-02   -4.06881235e-01  9.91284229e-01   -1.03401670e+02 -3.18844819e+01   -1.77149204e-01 -1.91056283e-01    4.93534660e+00 -1.21176945e+01   -2.26687358e+01  7.80719981e+00    1.89079281e-01  2.14601619e-01    2.26714306e+01 -7.80876257e+00   -6.51103717e+00  3.94473178e+00   -2.06755819e+02 -6.37150286e+01   -4.59950051e+01 -2.33848344e+02   -2.81808839e+00  1.62610452e+00    4.60017376e+01  2.33882017e+02   -1.89909157e+00  6.54054442e-01    1.58402688e-02  1.79784232e-02    1.89931733e+00 -6.54185363e-01
25663706e-01   -6.13224641e-01  1.48487870e+00   -1.03361572e+02 -3.20176693e+01   -2.66015636e-01 -2.86601209e-01    4.94218337e+00 -1.21191468e+01   -2.26726441e+01  7.78893119e+00    2.83640484e-01  3.22190563e-01    2.26787183e+01 -7.79244160e+00   -9.77383475e+00  5.90611528e+00   -2.06616215e+02 -6.39138757e+01   -4.58603329e+01 -2.33701846e+02   -4.23407113e+00  2.43848237e+00    4.58756320e+01  2.33777632e+02   -2.84912849e+00  9.78785961e-01    3.56433145e-02  4.04876603e-02    2.84989179e+00 -9.79227091e-01
67551608e-01   -8.22988640e-01  1.97587080e+00   -1.03303260e+02 -3.22004756e+01   -3.55233324e-01 -3.82217751e-01    4.95285811e+00 -1.21201958e+01   -2.26779991e+01  7.76332549e+00    3.78206693e-01  4.30108797e-01    2.26888245e+01 -7.76955068e+00   -1.30451829e+01  7.85401462e+00   -2.06416413e+02 -6.41847550e+01   -4.56742513e+01 -2.33496556e+02   -5.65881724e+00  3.24903205e+00    4.57018091e+01  2.33631373e+02   -3.79973522e+00  1.30075767e+00    6.33691396e-02  7.20654206e-02    3.80154903e+00 -1.30180071e+00
09439510e-01   -1.03718423e+00  2.46316400e+00   -1.03225264e+02 -3.24288807e+01   -4.44911834e-01 -4.78013515e-01    4.96826413e+00 -1.21196804e+01   -2.26846821e+01  7.73036044e+00    4.72750387e-01  5.38433294e-01    2.27016507e+01 -7.74005327e+00   -1.63275746e+01  9.78345672e+00   -2.06153491e+02 -6.45194539e+01   -4.54392559e+01 -2.33232371e+02   -7.09576230e+00  4.05538089e+00    4.54829870e+01  2.33443271e+02   -4.75106871e+00  1.61904290e+00    9.90126096e-02  1.12769205e-01    4.75462261e+00 -1.62107297e+00
51327412e-01   -1.25666623e+00  2.94549729e+00   -1.03126785e+02 -3.26973550e+01   -5.35136602e-01 -5.74161488e-01    4.98921342e+00 -1.21159044e+01   -2.26925395e+01  7.69001804e+00    5.67231767e-01  6.47203866e-01    2.27170680e+01 -7.70390980e+00   -1.96231042e+01  1.16891316e+01   -2.05825887e+02 -6.49067297e+01   -4.51586056e+01 -2.32909294e+02   -8.54834304e+00  4.85357087e+00    4.52226353e+01  2.33213586e+02   -5.70325724e+00  1.93271234e+00    1.42560892e-01  1.62660073e-01    5.70942190e+00 -1.93620371e+00
93215314e-01   -1.48204805e+00  3.42145622e+00   -1.03008611e+02 -3.29988923e+01   -6.25943558e-01 -6.70903620e-01    5.01613464e+00 -1.21065803e+01   -2.27013835e+01  7.64229221e+00    6.61614510e-01  7.56406733e-01    2.27349160e+01 -7.66108337e+00   -2.29332759e+01  1.35654238e+01   -2.05435235e+02 -6.53324145e+01   -4.48363508e+01 -2.32527564e+02   -1.00194405e+01  5.63769904e+00    4.49249277e+01  2.32942956e+02   -6.65639329e+00  2.24083711e+00    1.93995506e-01  2.21790038e-01    6.66622554e+00 -2.24634697e+00
35103216e-01   -1.71360622e+00  3.88953365e+00   -1.02874248e+02 -3.33254195e+01   -7.17286702e-01 -7.68539699e-01    5.04868185e+00 -1.20888822e+01   -2.27109950e+01  7.58719728e+00    7.55896964e-01  8.65960920e-01    2.27550037e+01 -7.61154701e+00   -2.62587948e+01  1.54065499e+01   -2.04988585e+02 -6.57802801e+01   -4.44773486e+01 -2.32087839e+02   -1.15104865e+01  6.39978222e+00    4.45946555e+01  2.32632587e+02   -7.61052746e+00  2.54249421e+00    2.53303504e-01  2.90186290e-01    7.62527493e+00 -2.55065389e+00
76991118e-01   -1.95119908e+00  4.34825572e+00   -1.02731109e+02 -3.36688023e+01   -8.09005399e-01 -8.67395216e-01    5.08529186e+00 -1.20596866e+01   -2.27211300e+01  7.52477630e+00    8.50161369e-01  9.75716749e-01    2.27771106e+01 -7.55529200e+00   -2.95993908e+01  1.72068329e+01   -2.04500708e+02 -6.62340949e+01   -4.40872367e+01 -2.31591438e+02   -1.30202840e+01  7.13006622e+00    4.42370857e+01  2.32284442e+02   -8.56566422e+00  2.83677383e+00    3.20503286e-01  3.67836549e-01    8.58676841e+00 -2.84827798e+00
...

后续你可以选择习惯的方式读取和处理。

# 可使用通配符简化输入，因为对应索引值下只会有一个文件
# 返回的是自定义类型的numpy数组
statsdata = pygrt.utils.read_statsfile(f"pygrtstats_{depsrc}_{deprcv}/K_0050_*")
print(statsdata.dtype)
# [('k', '<f8'), ('EX_q', '<c16'), ('EX_w', '<c16'), ('VF_q', '<c16'), ('VF_w', '<c16'), ('HF_q', '<c16'), ('HF_w', '<c16'), ('HF_v', '<c16'), ('DD_q', '<c16'), ('DD_w', '<c16'), ('DS_q', '<c16'), ('DS_w', '<c16'), ('DS_v', '<c16'), ('SS_q', '<c16'), ('SS_w', '<c16'), ('SS_v', '<c16')]

其中除了波数 k 外，每条结果的命名格式均为 {srcType}_{q/w/v}，与计算动态格林函数部分介绍的积分公式中的核函数 \(q_m, w_m, v_m\) 保持一致。

备注

核函数文件中记录的值非最终核函数值。对于动态解，还需乘 \(\left(-\dfrac{\Delta k}{4\pi\rho\omega^2}\right)\)。

可视化

以下将使用Python进行图件绘制。 在Python函数中指定震源类型、阶数、积分类型，可自动绘制核函数、被积函数和积分值随波数的变化，其中积分类型对应计算动态格林函数部分介绍的4种类型。

ir = 2
dist=distarr[ir]
srctype="SS"
ptype="0"
fig, ax = pygrt.utils.plot_statsdata(statsdata, dist=dist, srctype=srctype, ptype=ptype)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}.png", dpi=100)

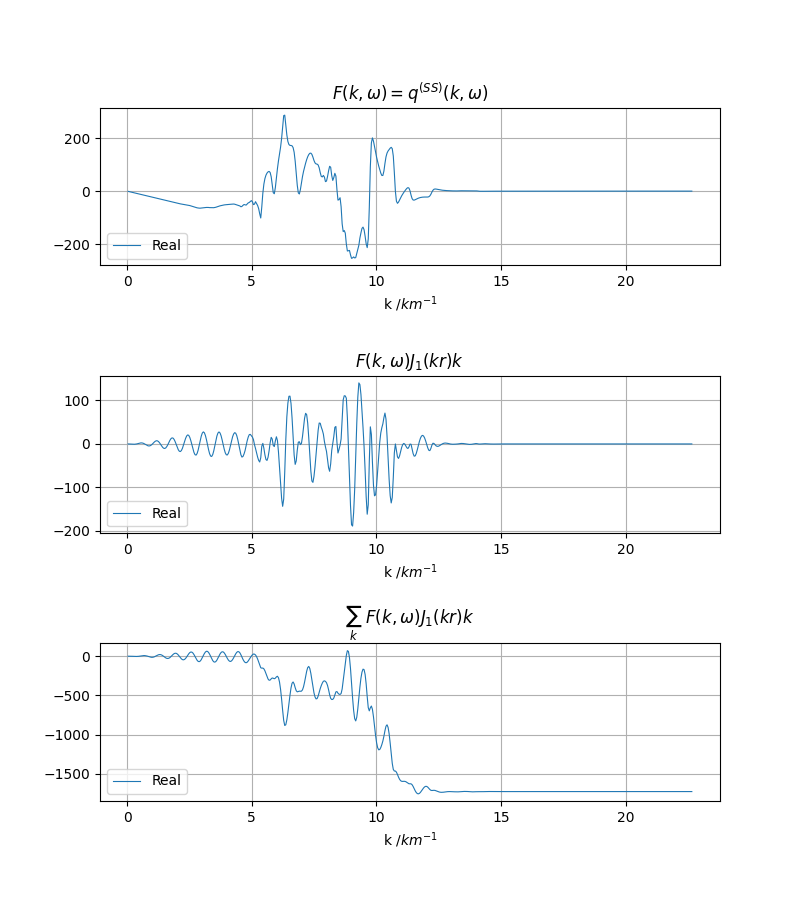
可以通过指定 RorI=False 参数来指定绘制虚部，传入 RorI=2 表示实虚部都绘制。

ir = 2
dist=distarr[ir]
srctype="SS"
ptype="0"
fig, ax = pygrt.utils.plot_statsdata(statsdata, dist=dist, srctype=srctype, ptype=ptype, RorI=2)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}_RI.png", dpi=100)

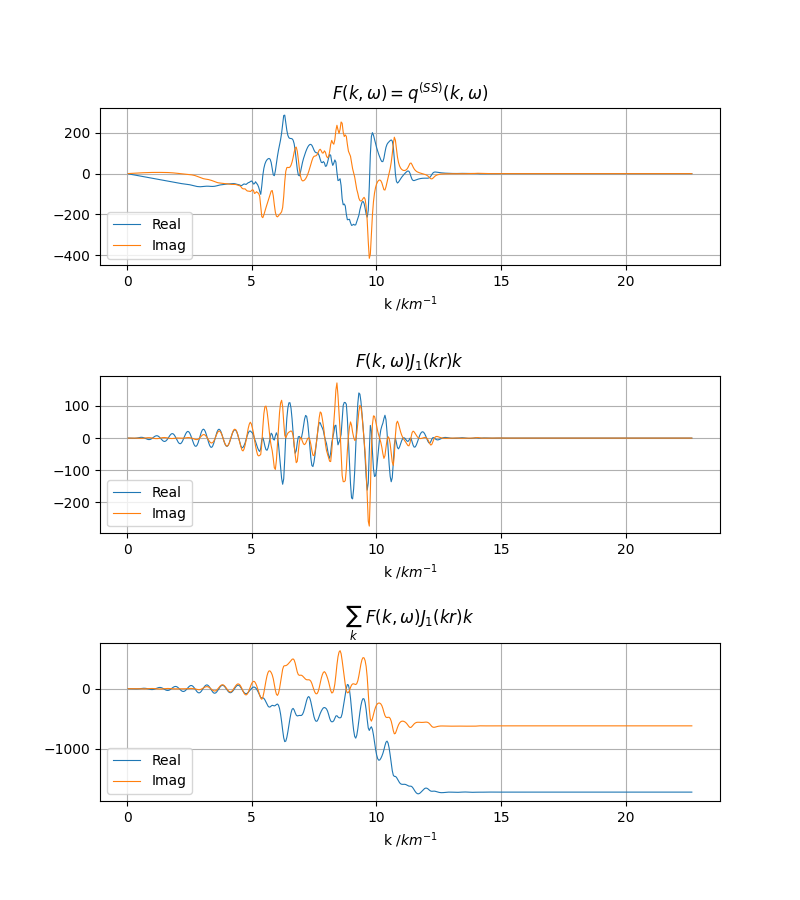
从图中可以看到，当波数增加到一定范围以上，积分收敛良好，无振荡现象。

当震源和场点深度接近/相等时，积分收敛速度变慢

假设其它参数不变，我们调整 震源深度为0.1km，再计算格林函数，读取核函数文件，绘制图像。

grt greenfn -Mmilrow -D0/0 -N500/0.02 -OGRN -R5,8,10 -S50,100
grt ker2asc GRN_grtstats/milrow_0_0/K_0050_5.00000e+00 > stats
# 绘制图像部分见Python

depsrc = 0.0
deprcv = 0.0
pymod = pygrt.PyModel1D(modarr, depsrc=depsrc, deprcv=deprcv)

stgrnLst = pymod.compute_grn(
    distarr=distarr, nt=500, dt=0.02,
    statsfile=f"pygrtstats_{depsrc}_{deprcv}", statsidxs=[50,100]
)

statsdata = pygrt.utils.read_statsfile(f"pygrtstats_{depsrc}_{deprcv}/K_0050_*")

dist=10
srctype="SS"
ptype="0"
fig, ax = pygrt.utils.plot_statsdata(statsdata, dist=dist, srctype=srctype, ptype=ptype, RorI=2)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}_{depsrc}_RI.png", dpi=100)

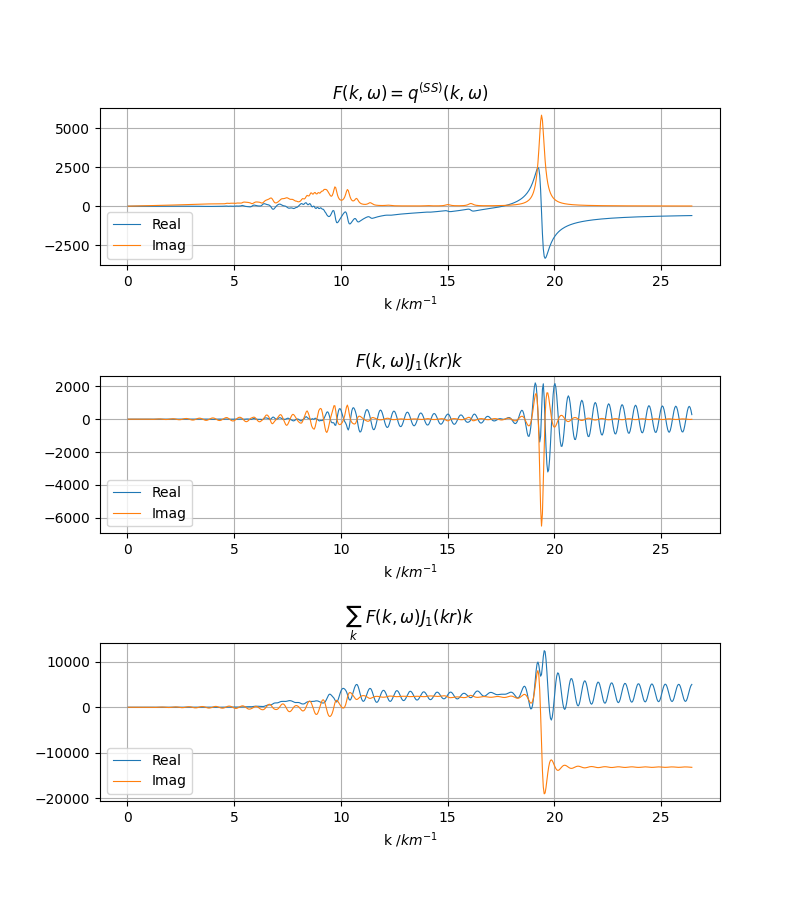
从图中可以清晰地看到，相比震源深度2km时，积分收敛速度明显变慢，积分值振荡，这要求增加波数积分上限，但这必然降低计算效率。

你可以尝试 当震源和场点位于同一深度，收敛振荡现象也很明显。要注意的是这和是否在地表无关，即使震源和场点都在地下，深度接近时积分收敛也会变慢。

峰谷平均法

具体原理很简洁易懂，从以下图像中你也能了解大概。详见 (Zhang et al., 2003) (张海明, 2021)。

在以上示例中，当震源和场点深度接近时，你会注意到输出的核函数文件增加了，这是因为程序内部设定 当震源和场点深度差小于1km时，自动使用峰谷平均法（PTAM）。具体流程为，程序中在进行完离散波数积分后，继续增加k（不同震中距使用不同dk），使用PTAM寻找足够数量的波峰和波谷（内部设定为36个），再对这些波峰波谷取缩减序列 \(M_i \leftarrow 0.5\times(M_i + M_{i+1})\) ，得到估计的积分收敛值。取缩减序列的C代码如下，

for(int n=n1; n>1; --n){
    for(int i=0; i<n-1; ++i){
        arr[i] = 0.5*(arr[i] + arr[i+1]);
    }
}

在 K_{iw}_{freq} 文件同级目录下，程序把 PTAM过程中的核函数以及积分峰谷位置分为两个文件 保存在 PTAM_{ir}_{dist}/ 目录下（ {ir} 为震中距索引， {dist} 为震中距），其中 PTAM_{ir}_{dist}/K_{iw}_{freq} 为核函数文件（格式不变）， PTAM_{ir}_{dist}/PTAM_{iw}_{freq} 为峰谷文件，其中记录积分值的峰谷。

备注

ker2asc 模块也支持将 PTAM_{ir}_{dist}/PTAM_{iw}_{freq} 文件转为文本格式，

grt ker2asc GRN_grtstats/milrow_0_0/PTAM_0002_1.00000e+01/PTAM_0050_5.00000e+00 > ptam_stats

输出的文件如下，

#                k                              EX_q                              EX_w                              VF_q                              VF_w                              HF_q                              HF_w                              HF_v                              DD_q                              DD_w                              DS_q                              DS_w                              DS_v                              SS_q                              SS_w                              SS_v
67622465e+01    6.56540447e+02 -6.56685940e+03    2.66053630e+01    1.35795580e+04  7.54745971e+02    2.67622568e+01   -6.79904618e+01  1.37174989e+03    2.66053633e+01   -1.96993245e+03 -3.58939919e+01    2.66053604e+01   -6.45663838e+02 -3.75692774e+02    2.67622542e+01   -1.01275137e+01  1.00693959e+01    2.67622568e+01    6.79904618e+01 -1.37174989e+03    2.66053605e+01    1.39523921e+03  8.58335768e+02    2.67622465e+01   -2.62616179e+03  2.62674376e+04    2.66053630e+01   -5.43182318e+04 -3.01898389e+03    2.65098060e+01    0.00000000e+00  0.00000000e+00    2.65098060e+01    0.00000000e+00  0.00000000e+00    2.65098060e+01    0.00000000e+00  0.00000000e+00    2.65098060e+01    0.00000000e+00  0.00000000e+00    2.67622465e+01    1.31308089e+03 -1.31337188e+04    2.66045993e+01   -4.12169613e+02 -2.42779393e+02    2.66046025e+01    2.71794665e+04  1.23488996e+03    2.67622465e+01   -1.80244975e+04  2.77976722e+04
70764072e+01    2.51518050e+03 -6.60974264e+03    2.69195212e+01    1.26908794e+04  7.87634819e+02    2.70764171e+01   -1.33187553e+02  1.37413124e+03    2.69195216e+01   -1.78972293e+03 -4.12001618e+01    2.69195189e+01   -5.06555790e+02 -3.78932149e+02    2.70764150e+01   -9.82636763e+00  1.00624197e+01    2.70764171e+01    1.33187553e+02 -1.37413124e+03    2.69195190e+01    1.61614488e+03  8.53196237e+02    2.70764072e+01   -1.00607220e+04  2.64389706e+04    2.69195212e+01   -5.07635177e+04 -3.15053928e+03    2.65883458e+01    0.00000000e+00  0.00000000e+00    2.65883458e+01    0.00000000e+00  0.00000000e+00    2.65883458e+01    0.00000000e+00  0.00000000e+00    2.65883458e+01    0.00000000e+00  0.00000000e+00    2.70764072e+01    5.03036100e+03 -1.32194853e+04    2.69187667e+01   -4.28530947e+02 -2.42399315e+02    2.69187695e+01    2.54018812e+04  1.30068019e+03    2.70764073e+01   -1.21219357e+04  2.76612826e+04
73905679e+01    6.63922165e+02 -6.56776606e+03    2.72336795e+01    1.35588833e+04  7.56334986e+02    2.73905774e+01   -7.01923475e+01  1.37188772e+03    2.72336799e+01   -1.96554741e+03 -3.61457771e+01    2.72336774e+01   -6.43462639e+02 -3.75801285e+02    2.73905757e+01   -1.01192231e+01  1.00691645e+01    2.73905774e+01    7.01923475e+01 -1.37188772e+03    2.72336775e+01    1.39878126e+03  8.58185575e+02    2.73905679e+01   -2.65568866e+03  2.62710642e+04    2.72336795e+01   -5.42355330e+04 -3.02533994e+03    2.66668856e+01    0.00000000e+00  0.00000000e+00    2.66668856e+01    0.00000000e+00  0.00000000e+00    2.66668856e+01    0.00000000e+00  0.00000000e+00    2.66668856e+01    0.00000000e+00  0.00000000e+00    2.73905679e+01    1.32784433e+03 -1.31355321e+04    2.72329339e+01   -4.12437856e+02 -2.42771055e+02    2.72329362e+01    2.71381020e+04  1.23806921e+03    2.73905680e+01   -1.79994311e+04  2.77953276e+04
77047285e+01    2.50887510e+03 -6.60893377e+03    2.75478378e+01    1.27097774e+04  7.86209928e+02    2.77047378e+01   -1.31157183e+02  1.37400760e+03    2.75478383e+01   -1.79379310e+03 -4.09736351e+01    2.75478359e+01   -5.08623107e+02 -3.78833808e+02    2.77047363e+01   -9.83427476e+00  1.00626416e+01    2.77047378e+01    1.31157183e+02 -1.37400760e+03    2.75478361e+01    1.61279151e+03  8.53335164e+02    2.77047285e+01   -1.00355004e+04  2.64357351e+04    2.75478378e+01   -5.08391095e+04 -3.14483971e+03    2.67454255e+01    0.00000000e+00  0.00000000e+00    2.67454255e+01    0.00000000e+00  0.00000000e+00    2.67454255e+01    0.00000000e+00  0.00000000e+00    2.67454255e+01    0.00000000e+00  0.00000000e+00    2.77047285e+01    5.01775019e+03 -1.32178675e+04    2.75471010e+01   -4.28273667e+02 -2.42407434e+02    2.75471029e+01    2.54396905e+04  1.29782936e+03    2.77047287e+01   -1.21441968e+04  2.76634249e+04
80188892e+01    6.69270525e+02 -6.56849017e+03    2.78619961e+01    1.35415605e+04  7.57618333e+02    2.80188982e+01   -7.20703622e+01  1.37199912e+03    2.78619967e+01   -1.96175764e+03 -3.63505303e+01    2.78619945e+01   -6.41515349e+02 -3.75890835e+02    2.80188970e+01   -1.01116777e+01  1.00689522e+01    2.80188982e+01    7.20703623e+01 -1.37199912e+03    2.78619946e+01    1.40196221e+03  8.58056686e+02    2.80188892e+01   -2.67708210e+03  2.62739607e+04    2.78619961e+01   -5.41662421e+04 -3.03047333e+03    2.68239653e+01    0.00000000e+00  0.00000000e+00    2.68239653e+01    0.00000000e+00  0.00000000e+00    2.68239653e+01    0.00000000e+00  0.00000000e+00    2.68239653e+01    0.00000000e+00  0.00000000e+00    2.80188892e+01    1.33854105e+03 -1.31369803e+04    2.78612679e+01   -4.12684655e+02 -2.42763185e+02    2.78612694e+01    2.71034445e+04  1.24063681e+03    2.80188894e+01   -1.79797190e+04  2.77933659e+04
83330498e+01    2.50438129e+03 -6.60828353e+03    2.81761545e+01    1.27256972e+04  7.85049382e+02    2.83330585e+01   -1.29415098e+02  1.37390681e+03    2.81761552e+01   -1.79733203e+03 -4.07877656e+01    2.81761531e+01   -5.10462284e+02 -3.78751904e+02    2.83330576e+01   -9.84147934e+00  1.00628443e+01    2.83330585e+01    1.29415098e+02 -1.37390681e+03    2.81761532e+01    1.60976858e+03  8.53455072e+02    2.83330498e+01   -1.00175252e+04  2.64331341e+04    2.81761545e+01   -5.09027890e+04 -3.14019753e+03    2.69025051e+01    0.00000000e+00  0.00000000e+00    2.69025051e+01    0.00000000e+00  0.00000000e+00    2.69025051e+01    0.00000000e+00  0.00000000e+00    2.69025051e+01    0.00000000e+00  0.00000000e+00    2.83330498e+01    5.00876257e+03 -1.32165671e+04    2.81754346e+01   -4.28036856e+02 -2.42415036e+02    2.81754358e+01    2.54715411e+04  1.29550748e+03    2.83330500e+01   -1.21615863e+04  2.76652250e+04
86472104e+01    6.72998358e+02 -6.56907568e+03    2.84903130e+01    1.35268953e+04  7.58671749e+02    2.86472189e+01   -7.36906788e+01  1.37209065e+03    2.84903137e+01   -1.95844405e+03 -3.65199298e+01    2.84903117e+01   -6.39773974e+02 -3.75966048e+02    2.86472181e+01   -1.01047941e+01  1.00687588e+01    2.86472189e+01    7.36906788e+01 -1.37209065e+03    2.84903119e+01    1.40483988e+03  8.57944843e+02    2.86472104e+01   -2.69199343e+03  2.62763027e+04    2.84903130e+01   -5.41075811e+04 -3.03468700e+03    2.69810449e+01    0.00000000e+00  0.00000000e+00    2.69810449e+01    0.00000000e+00  0.00000000e+00    2.69810449e+01    0.00000000e+00  0.00000000e+00    2.69810449e+01    0.00000000e+00  0.00000000e+00    2.86472104e+01    1.34599672e+03 -1.31381514e+04    2.84896011e+01   -4.12911972e+02 -2.42755857e+02    2.84896021e+01    2.70741042e+04  1.24274434e+03    2.86472106e+01   -1.79644510e+04  2.77917112e+04
89613710e+01    2.50134247e+03 -6.60775503e+03    2.88044714e+01    1.27392361e+04  7.84089903e+02    2.89613792e+01   -1.27904277e+02  1.37382339e+03    2.88044722e+01   -1.80044237e+03 -4.06328061e+01    2.88044703e+01   -5.12114829e+02 -3.78682575e+02    2.89613787e+01   -9.84806065e+00  1.00630286e+01    2.89613792e+01    1.27904277e+02 -1.37382339e+03    2.88044705e+01    1.60702479e+03  8.53559648e+02    2.89613710e+01   -1.00053699e+04  2.64310201e+04    2.88044714e+01   -5.09569443e+04 -3.13635961e+03    2.70595847e+01    0.00000000e+00  0.00000000e+00    2.70595847e+01    0.00000000e+00  0.00000000e+00    2.70595847e+01    0.00000000e+00  0.00000000e+00    2.70595847e+01    0.00000000e+00  0.00000000e+00    2.89613710e+01    5.00268495e+03 -1.32155101e+04    2.88037675e+01   -4.27818551e+02 -2.42422087e+02    2.88037682e+01    2.54986276e+04  1.29358791e+03    2.89613713e+01   -1.21749115e+04  2.76667484e+04
92755316e+01    6.75415340e+02 -6.56955375e+03    2.91186299e+01    1.35143714e+04  7.59548466e+02    2.92755395e+01   -7.51026933e+01  1.37216693e+03    2.91186308e+01   -1.95551771e+03 -3.66621676e+01    2.91186290e+01   -6.38202411e+02 -3.76030176e+02    2.92755392e+01   -1.00984974e+01  1.00685831e+01    2.92755395e+01    7.51026933e+01 -1.37216693e+03    2.91186292e+01    1.40745998e+03  8.57846838e+02    2.92755316e+01   -2.70166136e+03  2.62782150e+04    2.91186299e+01   -5.40574856e+04 -3.03819386e+03    2.71381245e+01    0.00000000e+00  0.00000000e+00    2.71381245e+01    0.00000000e+00  0.00000000e+00    2.71381245e+01    0.00000000e+00  0.00000000e+00    2.71381245e+01    0.00000000e+00  0.00000000e+00    2.92755316e+01    1.35083068e+03 -1.31391075e+04    2.91179337e+01   -4.13121732e+02 -2.42749081e+02    2.91179342e+01    2.70490484e+04  1.24449832e+03    2.92755318e+01   -1.79529089e+04  2.77903065e+04
...

记录了不同震源、不同积分类型的峰谷位置。

故为了绘制完整的波数积分+PTAM过程，涉及三个文件。不过Python函数已经做了优化，由于程序输出的目录结构固定，文件命名格式固定，只需传入 PTAM_{ir}_{dist}/PTAM_{iw}_{freq} 文件，Python函数会自动读取对应的三个文件。

ir = 2
statsdata1, statsdata2, ptamdata, dist = pygrt.utils.read_statsfile_ptam(f"pygrtstats_{depsrc}_{deprcv}/PTAM_{ir:04d}_*/PTAM_0050_*")

srctype="SS"
ptype="0"
fig, ax = pygrt.utils.plot_statsdata_ptam(statsdata1, statsdata2, ptamdata, dist=dist, srctype=srctype, ptype=ptype, RorI=2)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}_{depsrc}_ptam_RI.png", dpi=100)

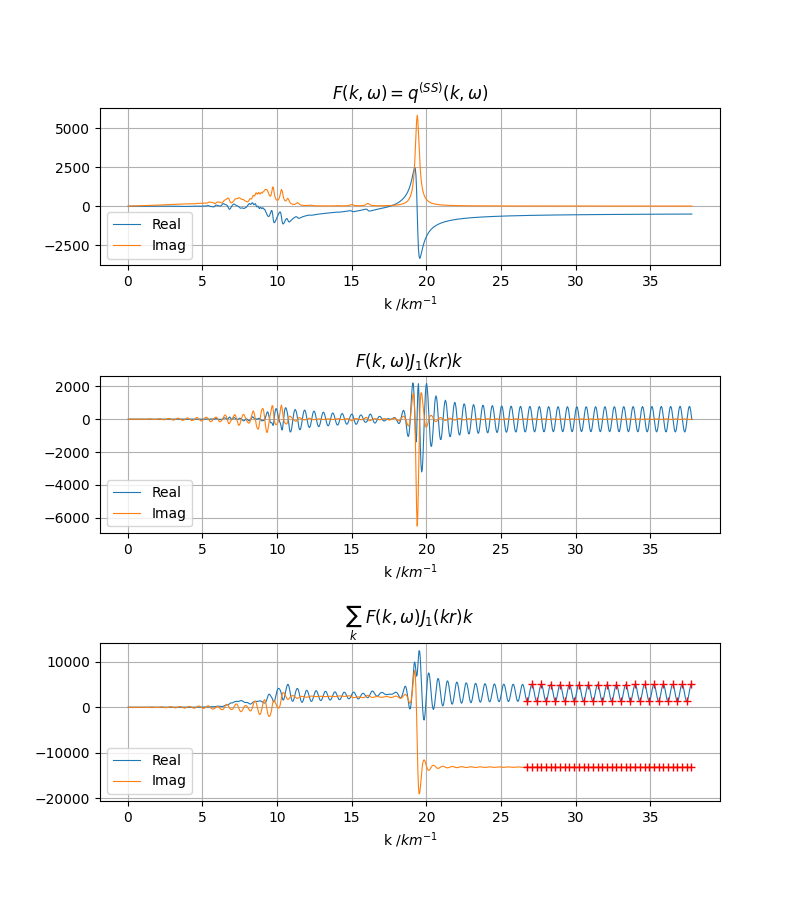
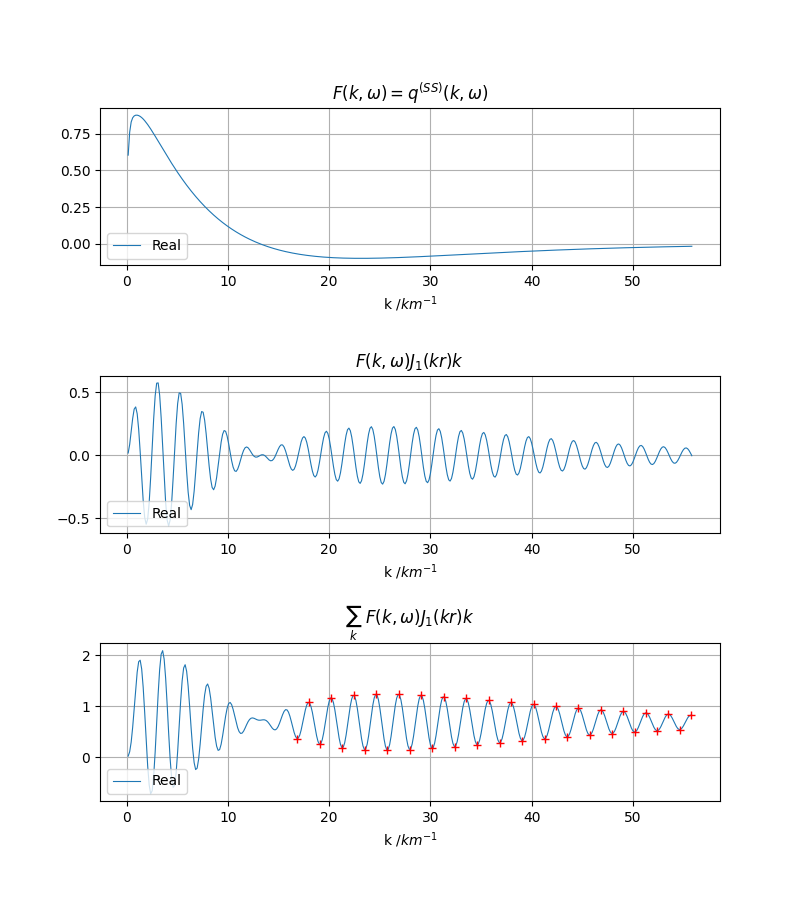
红十字为选取的波峰波谷，再取缩减序列即可得到估计的积分收敛值。

静态解的积分收敛性

以上部分是以动态解为例，静态解从积分类型、收敛特征、文件格式、绘图完全类似，只是不再有频率索引值。

备注

核函数文件中记录的值非最终核函数值。对于静态解，还需乘 \(\left(\dfrac{\Delta k}{4\pi\mu}\right)\)。

假设震源深度0.1km，场点位于地表，场点仅定义一个点(2,2)做示例，这里直接给出脚本。

# -S 表示输出核函数文件
grt static greenfn -Mmilrow -D0.1/0 -X2/2/1 -Y2/2/1 -S -Ostgrn.nc

# grt.ker2asc 也可以读取静态解输出的核函数文件，格式一致
grt ker2asc stgrtstats/milrow_0.1_0/K > static_stats

# 绘制图像部分见Python

import numpy as np
import pygrt 

modarr = np.loadtxt("milrow")

depsrc = 0.1
deprcv = 0.0
pymod = pygrt.PyModel1D(modarr, depsrc=depsrc, deprcv=deprcv)

xarr = np.array([2.0])
yarr = np.array([2.0])
static_grn = pymod.compute_static_grn(xarr, yarr, statsfile=f"static_pygrtstats_{depsrc}_{deprcv}")

ir = 0
statsdata1, statsdata2, ptamdata, dist = pygrt.utils.read_statsfile_ptam(f"static_pygrtstats_{depsrc}_{deprcv}/PTAM_{ir:04d}_*/PTAM")

srctype="SS"
ptype="0"
# 只使用离散波数积分的积分变化
fig, ax = pygrt.utils.plot_statsdata(statsdata1, dist=dist, srctype=srctype, ptype=ptype, RorI=True)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}_{depsrc}_static.png", dpi=100)

# 使用了峰谷平均法的积分变化
fig, ax = pygrt.utils.plot_statsdata_ptam(statsdata1, statsdata2, ptamdata, dist=dist, srctype=srctype, ptype=ptype, RorI=True)
fig.tight_layout()
fig.savefig(f"{srctype}_{ptype}_{depsrc}_ptam_static.png", dpi=100)

只使用离散波数积分

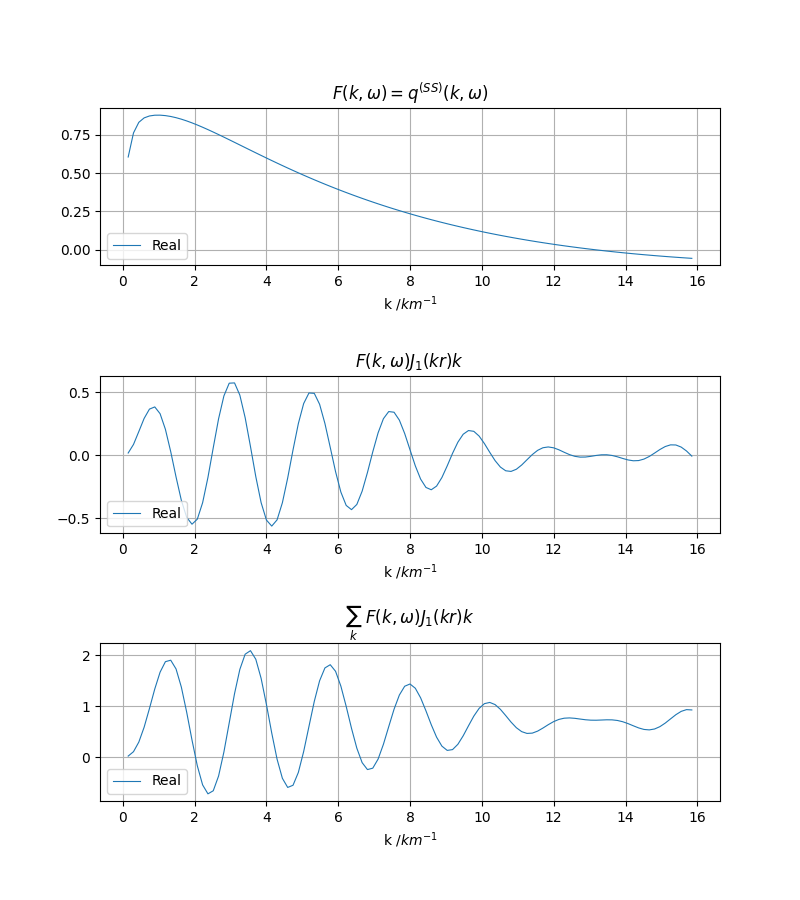
使用峰谷平均法