✍️ 朱邓达 • 📅 2025-04-20 • ⚡ 2025-12-05

核函数 \(f-v\) 谱图

在积分收敛性部分介绍了程序可以导出积分过程中不同频率的核函数值，这使得我们可以绘制核函数的 \(f-v\) 谱图 [1] ，以观察其中的频散特征。

以薄层模型为例，

01    1.5   0.18   1.78   1e4  1e4
01    1.7   0.35   1.85   1e4  1e4
02    1.6   0.25   1.80   1e4  1e4
00    2.0   0.6    1.94   1e4  1e4

生成核函数文件

备注

与之前的示例相比，这里添加了控制波数积分的参数，以显式控制核函数的采样间隔和范围。但这并非是计算格林函数的最佳参数，故此时格林函数计算结果很可能是不收敛的。这里的目的仅是提取特定范围内不同波数下的核函数。

# -S 后不指定索引表示输出所有频率点的核函数
# -K+v0.1 显式给定参考速度（用于定义波数积分上限），避免使用PTAM
# -L20 定义波数积分间隔dk
grt greenfn -Mmod1 -D0.03/0 -N500/0.02 -OGRN -R1 -K+v0.1 -S -L20

import numpy as np
import matplotlib.pyplot as plt
from typing import Union
import pygrt 

modarr = np.loadtxt("mod1")

pymod = pygrt.PyModel1D(modarr, depsrc=0.03, deprcv=0.0)

# 不指定statsidx，默认输出全部频率点的积分过程文件
# vmin_ref 显式给定参考速度（用于定义波数积分上限），避免使用PTAM
# Length 给定波数积分间隔dk
_ = pymod.compute_grn(distarr=[1], nt=500, dt=0.02, vmin_ref=0.1, Length=20, statsfile="pygrtstats")

读取，插值，获得 \(f-v\) 谱

Python端提供了 pygrt.utils.read_kernels_freqs() 函数来完成所有频率的核函数读取以及从波数 k 插值到特定速度点 v 的工作 ( \(v=\omega/k\) )，最后获得保存有核函数的 \(f-v\) 谱的字典。

# 指定待采样的速度数组
vels = np.arange(0.1, 0.6, 0.001)

# 读取所有频率的核函数，并插值到vels
# 不指定ktypes，默认返回全部核函数，均以2D数组的形式保存，shape=(nfreqs, nvels)
kerDct = pygrt.utils.read_kernels_freqs("pygrtstats", vels)
print(kerDct.keys())
# dict_keys(['_vels', '_freqs', 'EX_q', 'EX_w', 'VF_q', 'VF_w', 'HF_q', 'HF_w', 'HF_v', 'DD_q', 'DD_w', 'DS_q', 'DS_w', 'DS_v', 'SS_q', 'SS_w', 'SS_v'])

绘制核函数 \(f-v\) 谱图

以下将使用Python进行图件绘制。

# 绘制图像
def plot_kernel(kerDct:dict, RorI:bool, out:Union[str,None]=None):
    funcRorI = np.real if RorI else np.imag

    ktypes = []
    for key in kerDct:
        if key[0] == '_':
            continue
        ktypes.append(key)

    srctypes = ['EX', 'VF', 'HF', 'DD', 'DS', 'SS']

    vels = kerDct['_vels']
    freqs = kerDct['_freqs']

    fig = plt.figure(figsize=(12, 3*len(srctypes)))
    gs = fig.add_gridspec(len(srctypes), 3)
    qwvLst = ['q', 'w', 'v']
    for ik, key in enumerate(ktypes):
        srctype = key.split("_")[0]
        qwv = key.split("_")[1][0]
        
        ax = fig.add_subplot(gs[srctypes.index(srctype), qwvLst.index(qwv)])

        # 对不同速度间取归一化
        data = kerDct[key].copy()
        data[...] = data/np.max(np.abs(data), axis=1)[:,None]

        pcm = ax.pcolormesh(freqs, vels, np.abs(funcRorI(data)).T, vmin=0, vmax=1, shading='nearest')
        ax.set_xlabel("Frequency (Hz)")
        ax.set_ylabel("Velocity (km/s)")
        ax.set_title(key)
        fig.colorbar(pcm, ax=ax)

    if RorI:
        fig.suptitle("Real parts of Kernels", fontsize=20, x=0.5, y=0.99)
    else:
        fig.suptitle("Imag parts of Kernels", fontsize=20, x=0.5, y=0.99)

    if out is not None:
        fig.tight_layout()
        fig.savefig(out, dpi=100)


plot_kernel(kerDct, False, "imag.png")
plot_kernel(kerDct, True, "real.png")

虚部

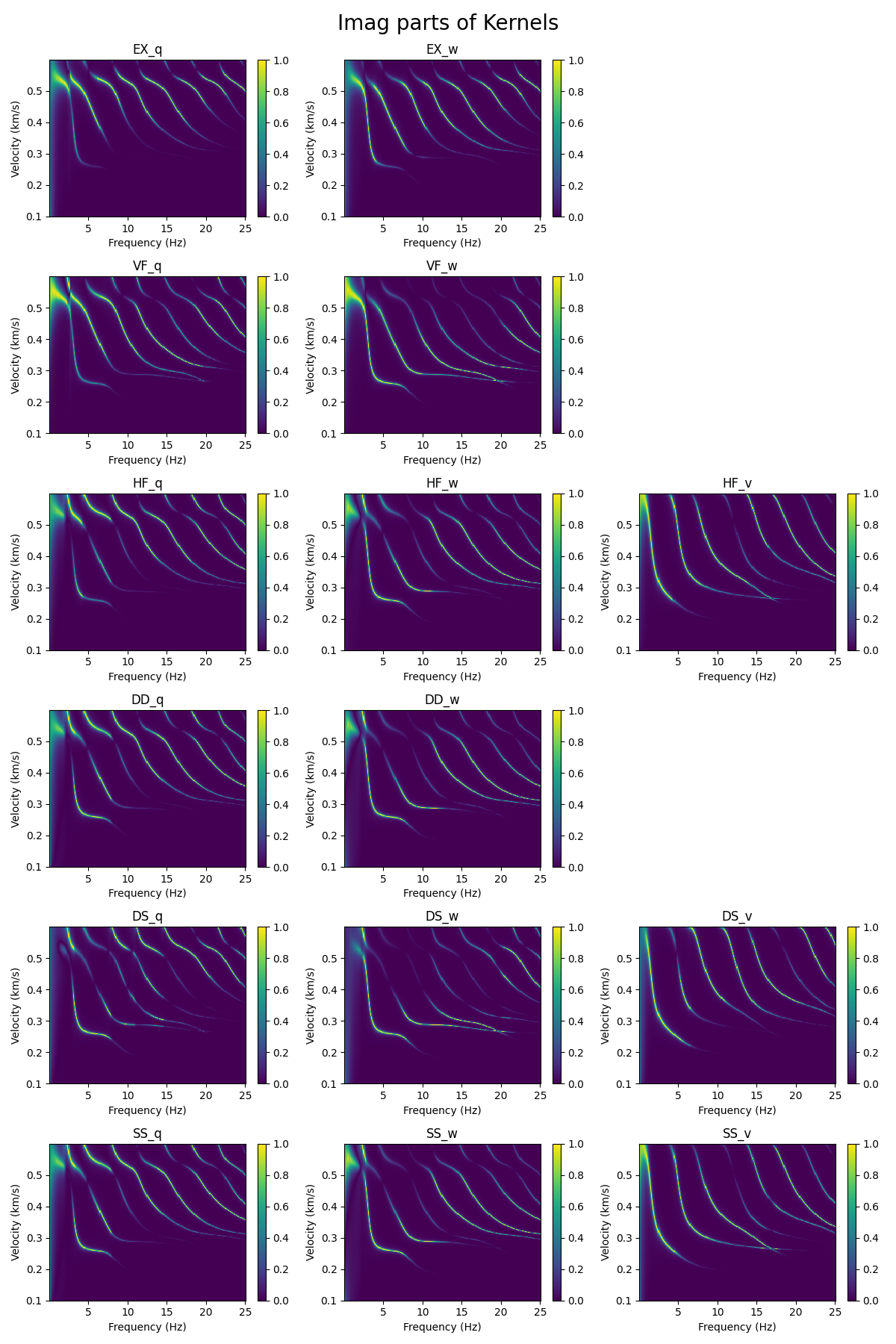
实部

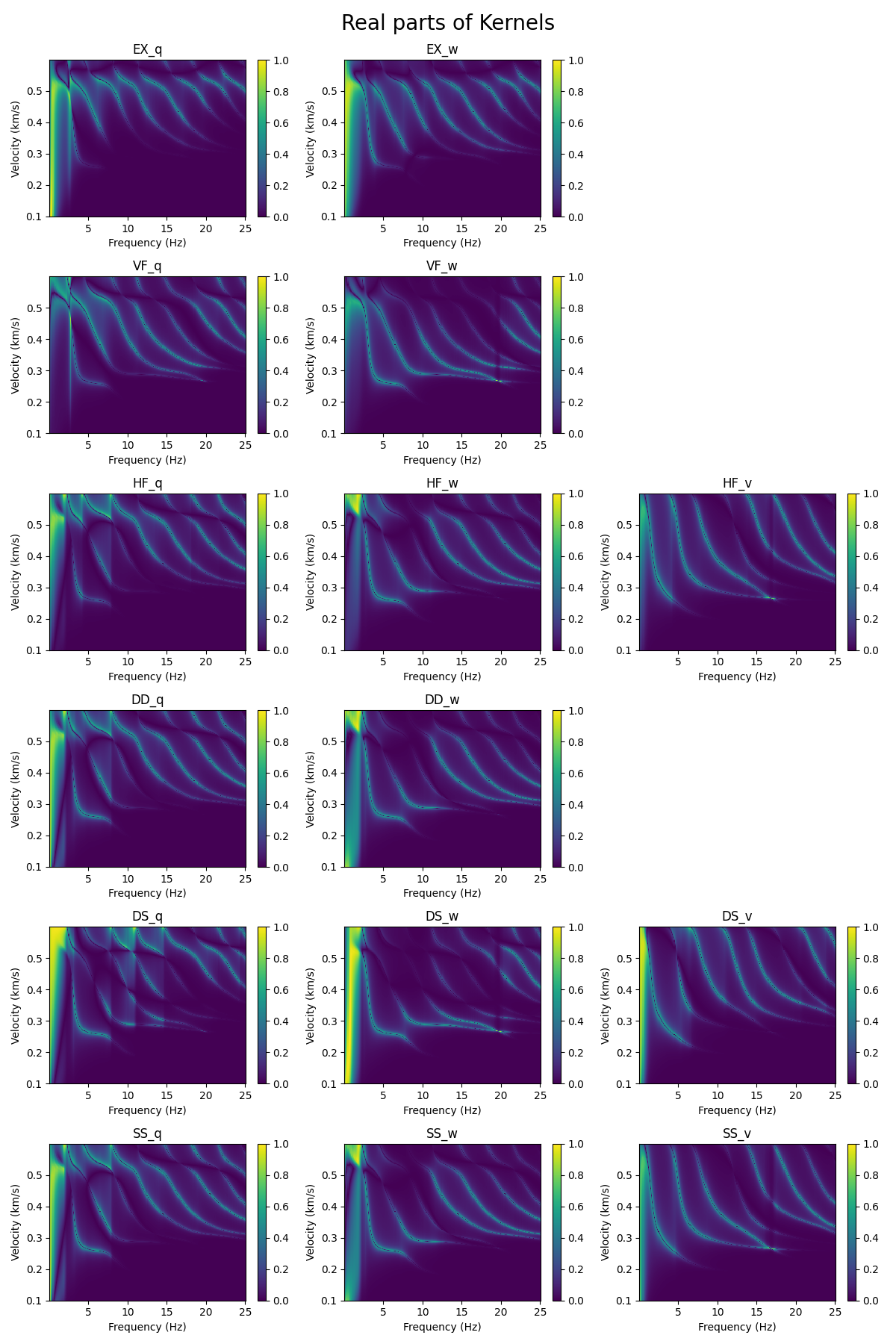
从图上可看到， 核函数 \(f-v\) 谱图的虚部峰值正是频散曲线的位置 ，尽管其中不同震源的核函数幅值不同，但 \(q_m，w_m\) 呈现的频散特征一致，这对应的是 Rayleigh波频散 ，而 \(v_m\) 对应的是 Love波频散 。

不同的震源场点深度、不同的虚频率都会导致幅值变化，积分间隔则会影响插值效果。

备注

注意其中仍然使用了虚频率，尽管这对于面波频散的分析引入了少许误差，但这使得 \(f-v\) 谱图中的高亮区域变宽，方便观察。