✍️ 朱邓达  •  📅 2025-04-17  •  ⚡ 2025-09-19

计算静态应变、旋转、应力张量

除了使用不同的函数名/程序名，输出文件不同之外，流程基本和 计算动态应变、旋转、应力张量 类似。这里直接给出脚本。

CPython

计算结果会以新增变量的形式直接写入 nc 网格，可使用 ncdump -h 查看。

#!/bin/bash
set -eu

rm -rf stgrn* stsyn* *.png

depsrc=2
deprcv=0

x1=-3
x2=3
dx=0.15

y1=-2.5
y2=2.5
dy=0.15
# -e 表示计算空间导数
grt static greenfn -Mmilrow -D${depsrc}/${deprcv} -X$x1/$x2/$dx -Y$y1/$y2/$dy -e -Ostgrn.nc

# -N 表示输出ZNE分量
grt static syn -S1e24 -M33/50/120 -e -N -Gstgrn.nc -Ostsyn_dc_zne.nc

# 计算应变
grt static strain stsyn_dc_zne.nc

# 计算旋转
grt static rotation stsyn_dc_zne.nc

# 计算应力
grt static stress stsyn_dc_zne.nc

---

---

---

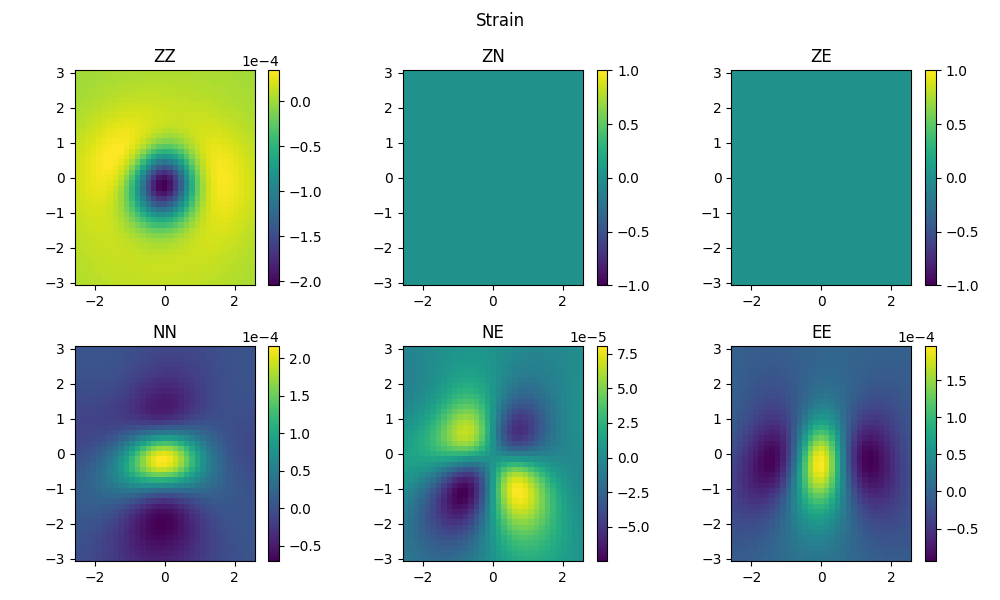
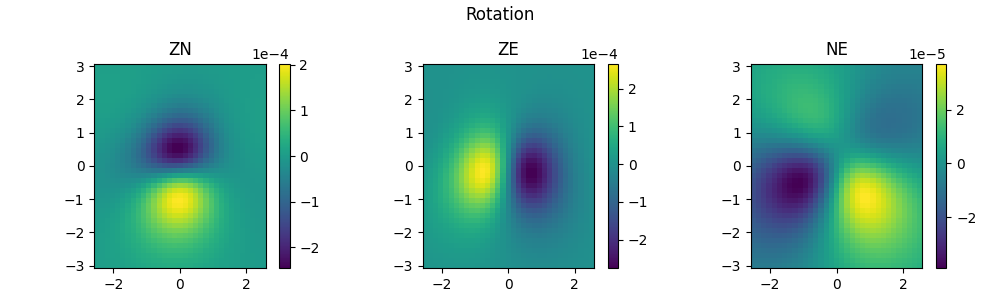
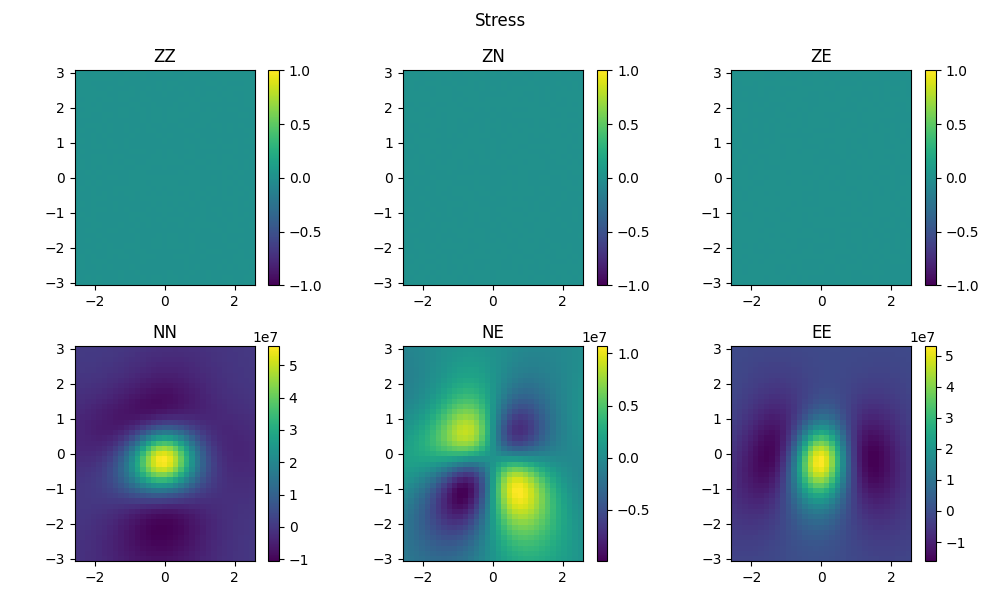
由于场点位于地表（自由表面），过Z平面的应力均为0（由于浮点数计算误差，呈极小非零数），结果和理论保持一致。