✍️ 朱邓达  •  📅 2025-04-17  •  ⚡ 2025-09-21

计算动态应变、旋转、应力张量

计算这些张量需要计算位移的空间导数 \(\partial z,\partial r,\partial \theta\) [1] 。 从前文关于格林函数的计算 （ 计算动态格林函数 ） 和位移合成的公式 （ 合成动态位移 ） 出发，位移空间导数分两个步骤计算，再根据几何方程和本构方程合成应变、旋转和应力张量。

[1]

\(\partial z,\partial r,\partial \theta\) 为 \(\dfrac{\partial}{\partial z},\dfrac{\partial}{\partial r},\dfrac{\partial}{\partial \theta}\) 的简写。

计算格林函数阶段，求出 \(\partial z,\partial r\)

假设在 milrow 模型中，震源深度2km，接收点位于地表，震中距为10km，计算格林函数及其空间导数，要求采样点数500个点，采样间隔0.02s。

CPython

# -e 表示计算空间导数
grt greenfn -Mmilrow -D2/0 -N500/0.02 -OGRN -R10 -e

在 GRN/milrow_{depsrc}_{deprcv}_{dist}/ 路径下，文件名开头有”r”和”z”就代表 \(\partial r\) 和 \(\partial z\)。

备注

计算格林函数阶段求出的空间导数的单位：

• 爆炸源： \(10^{-25} \, /\text{dyne} \cdot \text{cm}\)

• 单力源： \(10^{-20} \, /\text{dyne}\)

• 剪切源： \(10^{-25} \, /\text{dyne} \cdot \text{cm}\)

• 矩张量源： \(10^{-25} \, /\text{dyne} \cdot \text{cm}\)

合成位移阶段，求出 \(\partial \theta / r\) 并合成位移空间导数

假设震源为剪切源，断层走向33°，倾角50°，滑动角120°，标量矩 1e24 dyne·cm，方位角30°。待求项中有 \(r\) 是为了保证量纲统一。

CPython

# -e 表示计算空间导数
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -M33/50/120 -Osyn_dc -e

在 syn_dc/ 路径下，文件名开头有”r”，”z”，”t”分别代表 \(\partial r\)， \(\partial z\)，\(\partial \theta / r\)。

以上计算的空间导数在柱坐标系下，即 \(\dfrac{\partial u(z,r,\theta)}{\partial(z,r,\theta)}\)。如果需要 \(\dfrac{\partial u(z,x,y)}{\partial(z,x,y)}\) （ \(x\) 表示北向， \(y\) 表示东向），传入适当参数即可，则输出结果开头的标识符从”z/r/t”变为”z/x/y”。

CPython

# -N 表示输出ZNE分量
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -M33/50/120 -Osyn_dc_zne -e -N

在 syn_dc_zne/ 路径下，文件名开头有”z”，”n”，”e”分别代表 \(\partial z\)， \(\partial x\)，\(\partial y\)。

备注

合成的位移空间导数单位为1。

合成应变、旋转、应力张量

应变和应力均为二阶对称张量，故将输出6个独立分量；而旋转张量为二阶反对称张量，将输出3个独立分量。

程序选择张量输出结果的坐标系的依据是——根据文件名/通道名判断是否存在 \(\dfrac{\partial u_x}{\partial x}\)，如果有则使用ZNE坐标系，否则使用ZRT坐标系。 所以建议保存结果的文件夹中只使用同种坐标系，就像上面分为 syn_dc/ 和 syn_dc_zne/ 两个文件夹保存。

以下绘图使用Python绘制，绘图函数如下：

from obspy import *
import matplotlib.pyplot as plt

def plot6(st6:Stream, title:str, out:str|None=None):
    nt = st6[0].stats.npts
    dt = st6[0].stats.delta
    t = np.arange(nt)*dt

    MAX, MIN = 0, 9e30
    for tr in st6:
        d = np.abs(tr.data)
        if MAX < np.max(d):
            MAX = np.max(d)
        if MIN > np.min(d):
            MIN = np.min(d)

    travtP = stsyn[0].stats.sac['t0']
    travtS = stsyn[0].stats.sac['t1']

    fig, axs = plt.subplots(len(st6), 1, figsize=(10, 1.2*len(st6)), gridspec_kw=dict(hspace=0.0), sharex=True)
    for i in range(len(st6)):
        tr = st6[i]
        ax = axs[i]

        ax.plot(t, tr.data, c='k', lw=0.5, label=tr.stats.channel)
        ax.legend(loc='upper left')

        ylims = ax.get_ylim()
        if np.max(np.abs(np.array(ylims)))/MAX < 1e-5:
            ylims = [-1, 1]
            ax.set_ylim(ylims)
            
        # 绘制到时
        ax.vlines(travtP, *ylims, colors='b')
        ax.text(travtP, ylims[1], "P", ha='left', va='top', color='b')
        ax.vlines(travtS, *ylims, colors='r')
        ax.text(travtS, ylims[1], "S", ha='left', va='top', color='r')

        ax.set_xlim([t[0], t[-1]])
        ax.set_ylim(np.array(ylims)*1.2)

    fig.suptitle(title)

    if out is not None:
        fig.tight_layout()
        fig.savefig(out, dpi=100)

应变张量

根据几何方程（应变-位移关系） [2]

\[e_{ij} = \dfrac{1}{2} \left( u_{i,j} + u_{j,i} \right) = \dfrac{1}{2} \left( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i} \right)\]

CPython

# 指定文件夹，会在原文件夹内输出SAC格式的应变张量
grt strain syn_dc_zne

在 syn_dc_zne/ 原路径下，生成 strain_??.sac，文件名中包括分量名，如ZZ、ZN等。

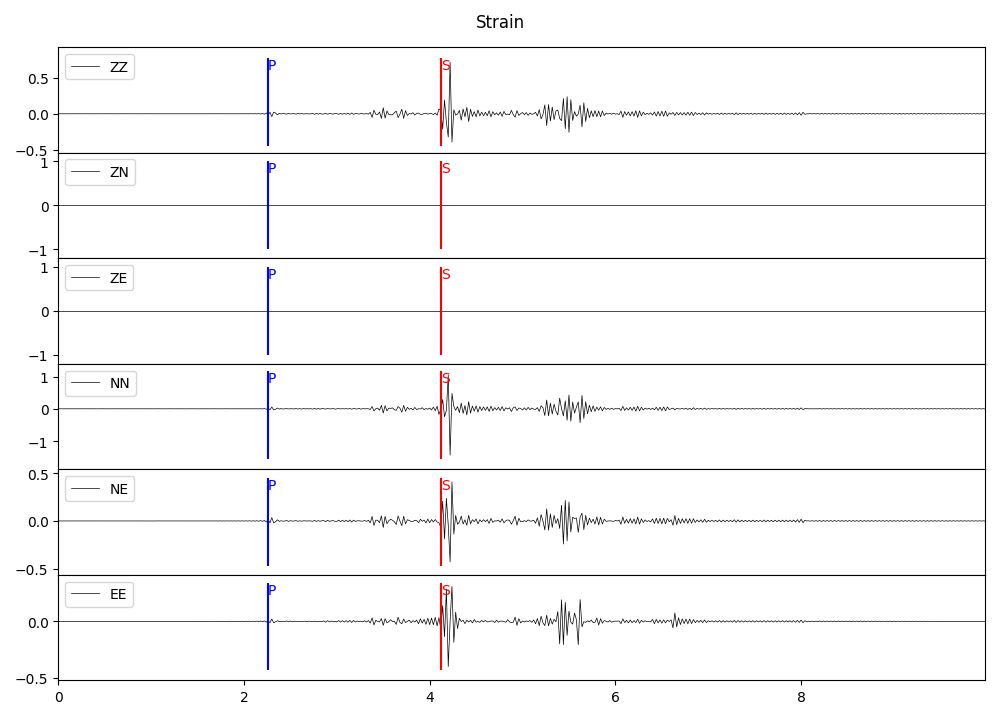
旋转张量

根据旋转-位移关系 [2]

\[w_{ij} = \dfrac{1}{2} \left( u_{i,j} - u_{j,i} \right) = \dfrac{1}{2} \left( \dfrac{\partial u_i}{\partial x_j} - \dfrac{\partial u_j}{\partial x_i} \right)\]

CPython

# 指定文件夹，会在原文件夹内输出SAC格式的旋转张量
grt rotation syn_dc_zne

在 syn_dc_zne/ 原路径下，生成 rotation_??.sac，文件名中包括分量名，如ZN，ZE，NE。

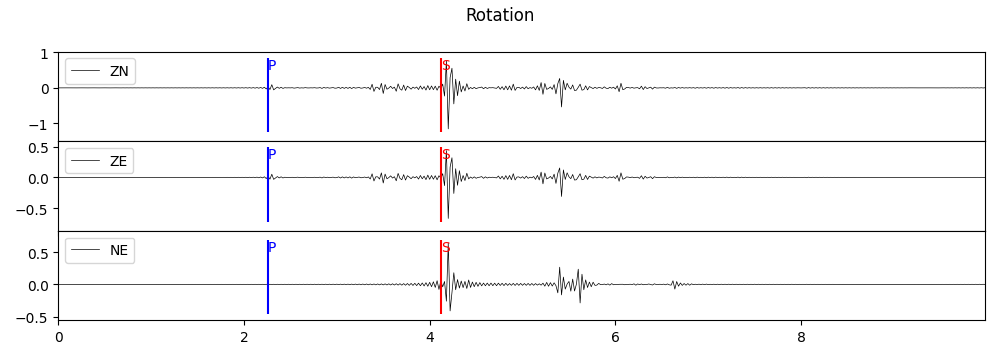
应力张量

根据各向同性介质的本构方程 [2]

\[\sigma_{ij} = \lambda \delta_{ij} e_{kk} + 2 \mu e_{ij} = \lambda \delta_{ij} u_{kk} + \mu \left( u_{i,j} + u_{j,i} \right)\]

CPython

# 指定文件夹，会在原文件夹内输出SAC格式的应力张量
grt stress syn_dc_zne

在 syn_dc_zne/ 原路径下，生成 stress_??.sac，文件名中包括分量名，如ZZ、ZN等。

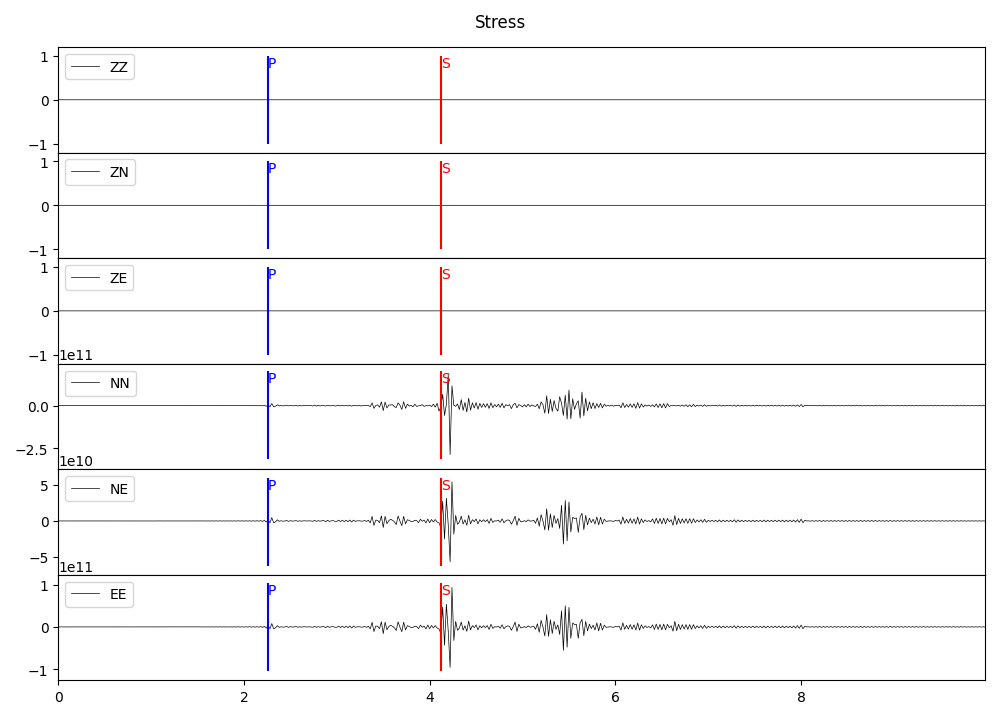
备注

计算得到的应力的单位为 \(\frac{\text{dyne}}{\text{cm}^2} = 0.1 \text{Pa}\)。

由于场点位于地表（自由表面），过Z平面的应力均为0（由于浮点数计算误差，呈极小非零数），结果和理论保持一致。

[2] (1,2,3)

这只适用于ZNE坐标系，对于ZRT坐标系需考虑协变导数。程序中已考虑，这里不再做公式介绍。