✍️ 朱邓达  •  📅 2025-04-17  •  ⚡ 2025-09-22

合成动态位移

警告

震源机制参数中（如单力源、矩张量源）Z轴取向下为正。

Python中合成动态位移的主函数为 gen_syn_from_gf_*() （*表示对不同震源） ，C模块为 syn。

使用上节计算的格林函数，合成动态位移（理论地震图）。方便起见，这里统一使用milrow模型，震源深度2km，场点位于地表，震中距10km的格林函数，方位角30°。

在已知三分量格林函数 \(W_m(t), Q_m(t), V_m(t)\) 后，合成三分量位移 \(u_z(t), u_r(t), u_\theta (t)\) 的公式为

\[\begin{split}\left\{ \begin{aligned} u_z(t) &= D(t) * \left[ \sum_{m=0}^{m=2} A_m W_m(t) \right] \\ u_r(t) &= D(t) * \left[ \sum_{m=0}^{m=2} A_m Q_m(t) \right] \\ u_\theta (t) &= D(t) * \left[ \sum_{m=1}^{m=2} A_{m+3} V_m(t) \right] \end{aligned} \right.\end{split}\]

其中 \(D(t)\) 为震源时间函数，\(*\) 表示卷积，\(A_m\) 为与方位角和震源机制相关的方向因子，其中 \(u_z, u_r\) 的方向因子相同，而 \(u_\theta\) 的方向因子满足

\[A_{m+3} = \frac{d A_m}{d (m\theta)}, m=1,2\]

其中 \(m\) 为阶数，\(\theta\) 为方位角。

备注

合成位移的结果单位为 \(\text{cm}\)。

不同震源

以下绘图使用Python绘制，绘图函数如下：

from obspy import *
import matplotlib.pyplot as plt
from typing import Union

def plot_syn(stsyn:Stream, out:Union[str,None]=None, sigs:Union[np.ndarray,None]=None):
    figsize = (10, 4)
    nrow = 3
    if sigs is not None:
        nrow += 1
        figsize = (10, 4.5)

    fig, axs = plt.subplots(nrow, 1, figsize=figsize, gridspec_kw=dict(hspace=0.0), sharex=True)
    nt = stsyn[0].stats.npts
    dt = stsyn[0].stats.delta
    t = np.arange(nt)*dt

    if sigs is not None:
        ax = axs[0]
        ax.plot(t[:len(sigs)], sigs, 'k-', lw=0.5)
        axs = axs[1:]

    travtP = stsyn[0].stats.sac['t0']
    travtS = stsyn[0].stats.sac['t1']

    for i, tr in enumerate(stsyn):
        ax = axs[i]
        ax.plot(t, tr.data, c='k', lw=0.5, label=tr.stats.channel)
        ax.legend(loc='upper left')

        ylims = ax.get_ylim()
        # 绘制到时
        ax.vlines(travtP, *ylims, colors='b')
        ax.text(travtP, ylims[1], "P", ha='left', va='top', color='b')
        ax.vlines(travtS, *ylims, colors='r')
        ax.text(travtS, ylims[1], "S", ha='left', va='top', color='r')

        ax.set_xlim([t[0], t[-1]])
        ax.set_ylim(np.array(ylims)*1.2)

    if out is not None:
        fig.tight_layout()
        fig.savefig(out, dpi=100)

def plot_int_dif(stsyn:Stream, stsyn_int:Stream, stsyn_dif:Stream, comp:str, out:Union[str,None]=None):
    nt = stsyn[0].stats.npts
    dt = stsyn[0].stats.delta
    t = np.arange(nt)*dt

    travtP = stsyn[0].stats.sac['t0']
    travtS = stsyn[0].stats.sac['t1']

    fig, axs = plt.subplots(3, 1, figsize=(10, 4), gridspec_kw=dict(hspace=0.0), sharex=True)
    for i, (st, suffix) in enumerate(zip([stsyn, stsyn_int, stsyn_dif], ["", "_int", "_dif"])):
        tr = st.select(component=comp)[0]

        ax = axs[i]
        ax.plot(t, tr.data, c='k', lw=0.5, label=f"{tr.stats.channel}{suffix}")
        ax.legend(loc='upper left')

        ylims = ax.get_ylim()
        # 绘制到时
        ax.vlines(travtP, *ylims, colors='b')
        ax.text(travtP, ylims[1], "P", ha='left', va='top', color='b')
        ax.vlines(travtS, *ylims, colors='r')
        ax.text(travtS, ylims[1], "S", ha='left', va='top', color='r')

        ax.set_xlim([t[0], t[-1]])
        ax.set_ylim(np.array(ylims)*1.2)

        if out is not None:
            fig.tight_layout()
            fig.savefig(out, dpi=100)

爆炸源

标量矩 1e24 dyne·cm。

CPython

# 合成结果在 syn_ex/ 目录下，以SAC格式保存。
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -Osyn_ex

单力源

北向力 \(f_N=1\)，东向力 \(f_E=-0.5\)，垂直向下的力 \(f_Z=2\)，单位 1e16 dyne。

CPython

# 合成结果在 syn_sf/ 目录下，以SAC格式保存。
grt syn -GGRN/milrow_2_0_10 -S1e16 -A30 -F1/-0.5/2 -Osyn_sf

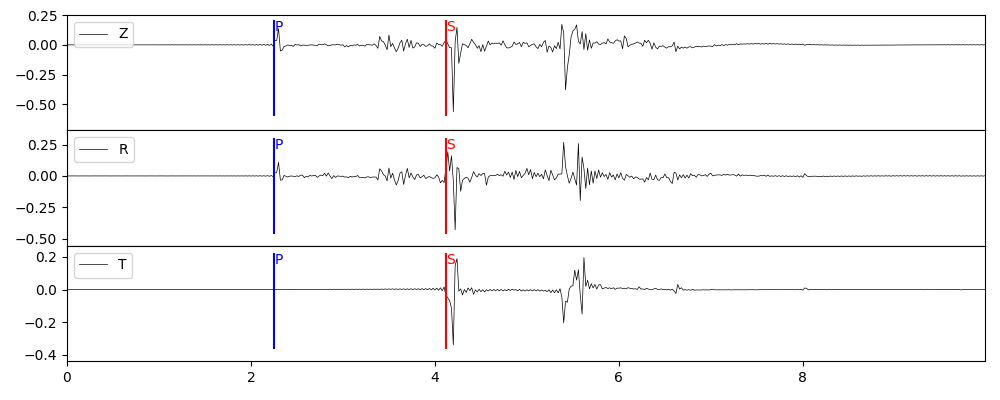
剪切源

断层走向33°，倾角50°，滑动角120°，标量矩 1e24 dyne·cm。

CPython

# 合成结果在 syn_dc/ 目录下，以SAC格式保存。
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -M33/50/120 -Osyn_dc

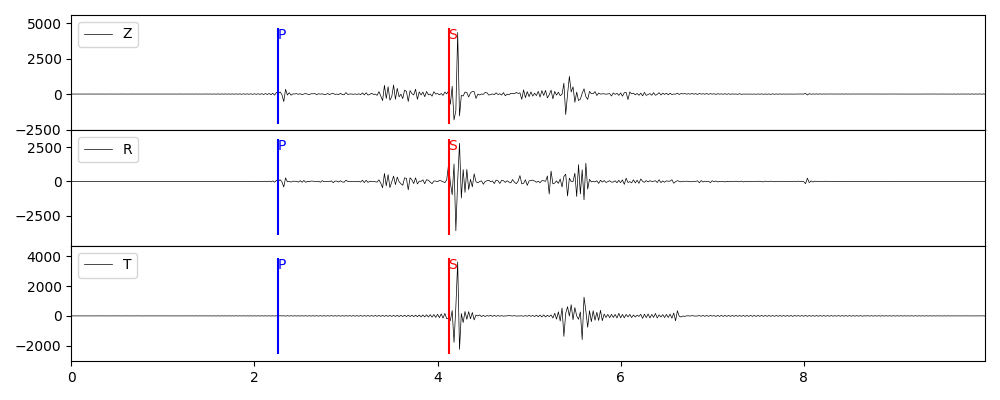
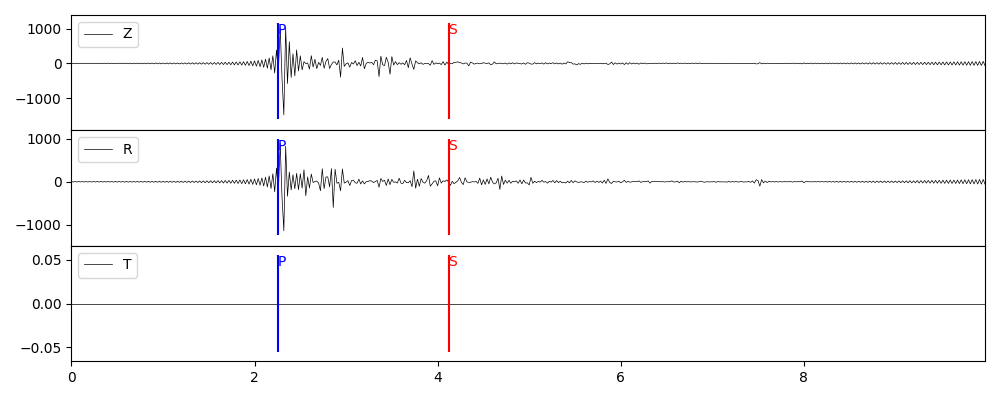
矩张量源

\(M_{xx}=0.1, M_{xy}=-0.2, M_{xz}=1.0, M_{yy}=0.3, M_{yz}=-0.5, M_{zz}=-2.0\)，单位 1e24 dyne·cm， 其中X为北向，Y为东向，Z为垂直向下。

CPython

# 合成结果在 syn_mt/ 目录下，以SAC格式保存。
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -T0.1/-0.2/1.0/0.3/-0.5/-2.0 -Osyn_mt

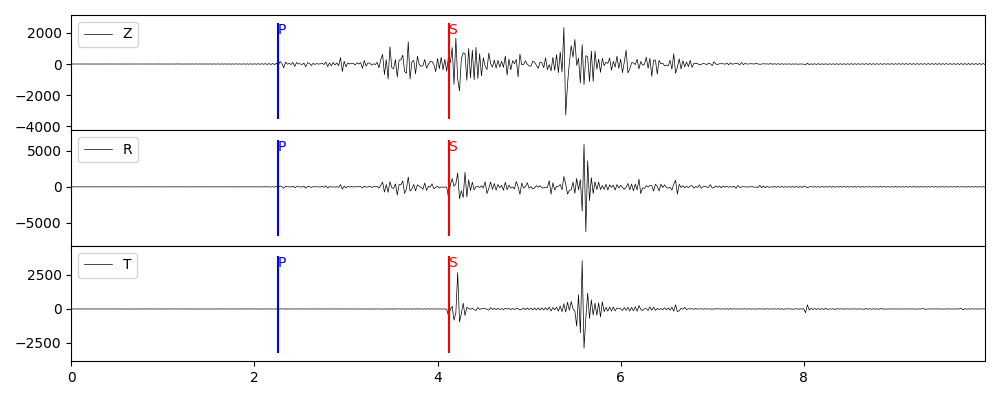
分量旋转

PyGRT 计算默认输出为ZRT分量（柱坐标系），可以设置参数以输出ZNE分量，这里以剪切源为例，

CPython

# 传入-N可输出ZNE分量
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -M33/50/120 -Osyn_dc_zne -N

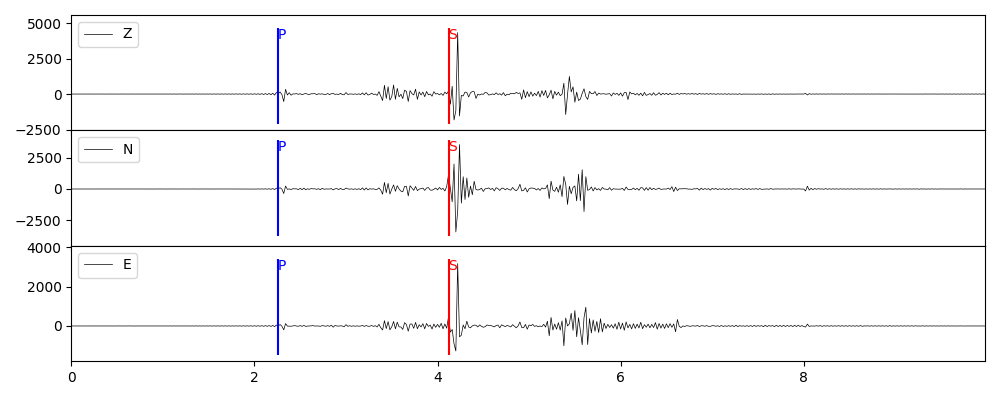
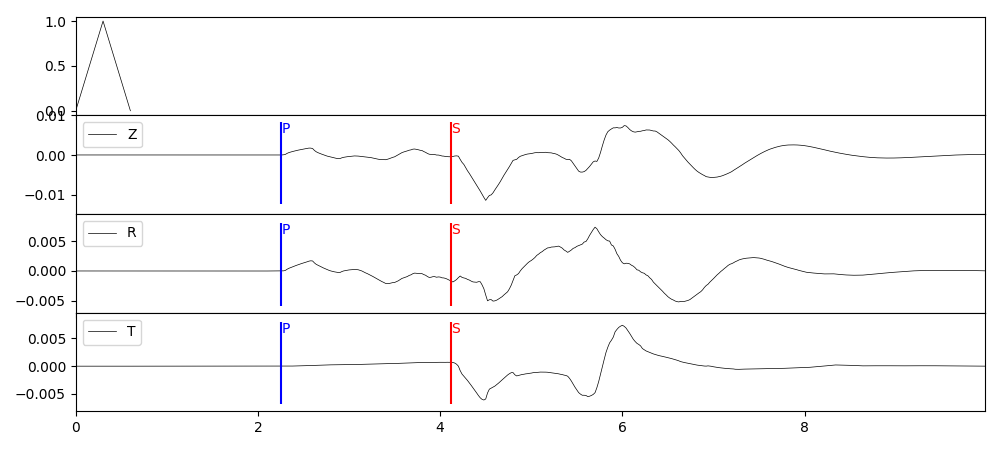
卷积时间函数

PyGRT 内置了一些震源时间函数，例如抛物波、梯形波、雷克子波或自定义，这里以单力源为例。

CPython

# -Dt定义梯形波的三个时间参数，爬升截止时刻/平稳截止时刻/结束时刻
# 前两个时刻重合则退化为三角波
grt syn -GGRN/milrow_2_0_10 -S1e16 -A30 -F1/-0.5/2 -Osyn_sf_trig -Dt/0.3/0.3/0.6

生成的时间函数会以SAC格式保存在对应路径中，文件名为 sig.sac。 其它时间函数以及具体参数用法详见 syn 模块。

位移对时间积分、微分

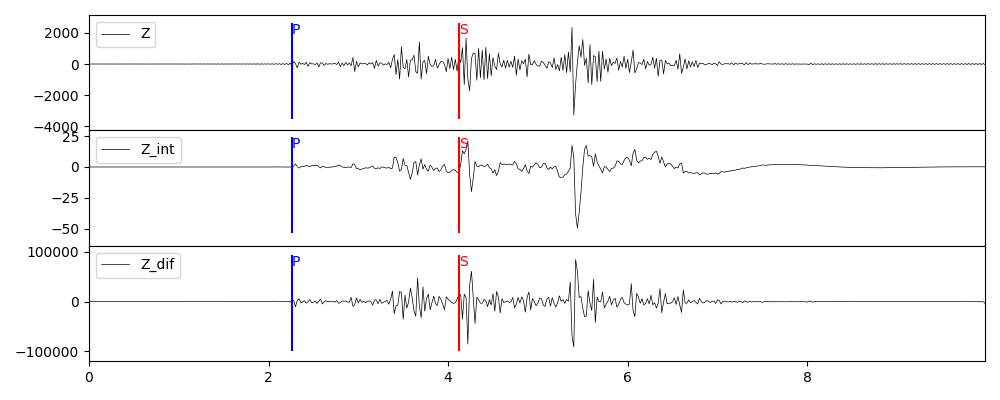
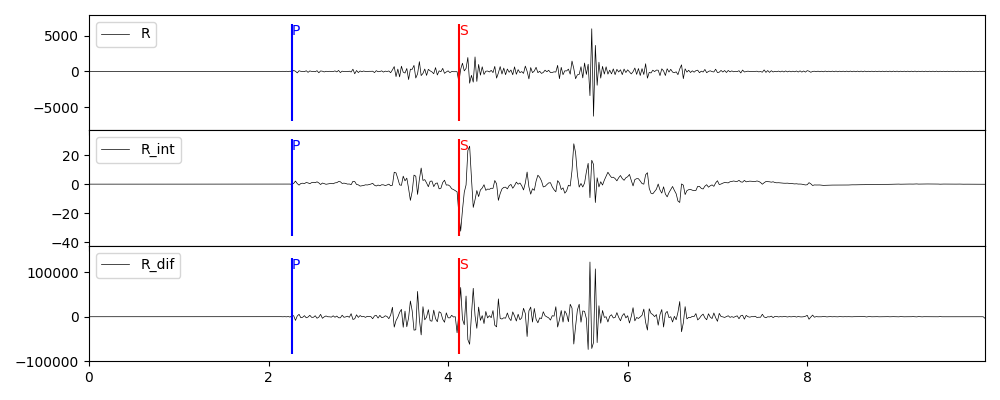
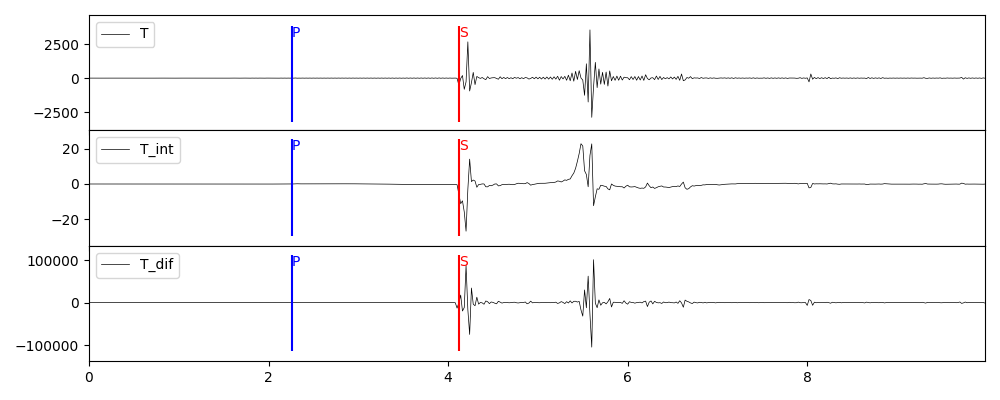
这里以矩张量源为例。

CPython

# 积分，1表示积分1次
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -T0.1/-0.2/1.0/0.3/-0.5/-2.0 -I1 -Osyn_mt_int1
# 微分，1表示微分1次
grt syn -GGRN/milrow_2_0_10 -S1e24 -A30 -T0.1/-0.2/1.0/0.3/-0.5/-2.0 -J1 -Osyn_mt_dif1