合成静态位移
Python中合成静态位移的主函数为 gen_syn_from_gf_*() (*表示对不同震源)(与合成动态位移的函数共用) ,C模块为 static_syn。
使用上节计算的格林函数,合成静态位移。为方便画图,以下结果都使用ZNE分量。
不同震源
以下绘图使用 GMT 绘制。这里提供计算和绘图的 Python 脚本和 Shell 脚本供下载参考。
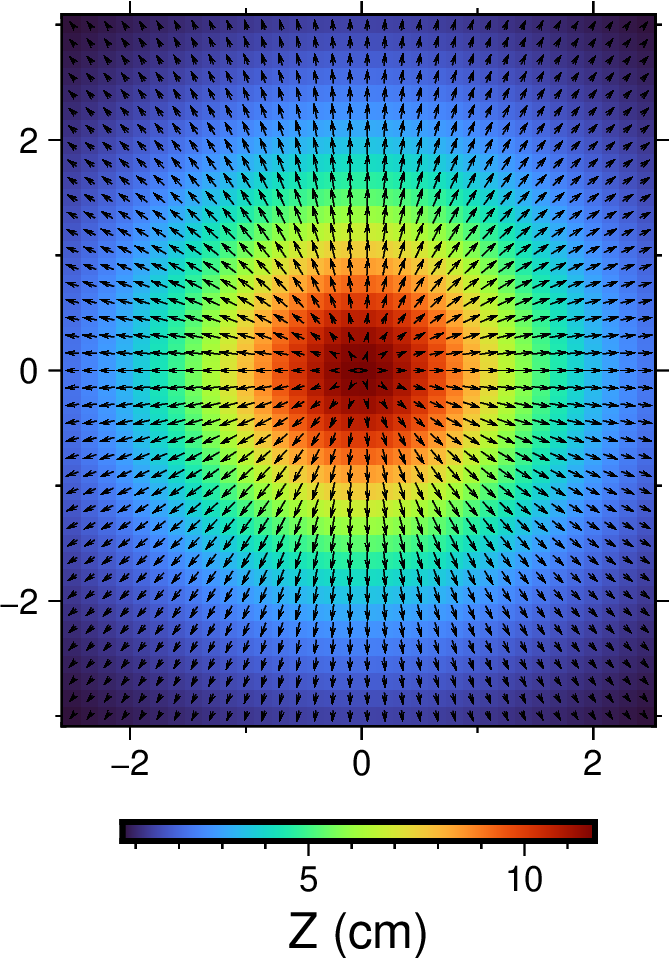
爆炸源
标量矩 1e24 dyne·cm。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e24 -N -Gstgrn.nc -Ostsyn_ex.nc
static_syn = pygrt.utils.gen_syn_from_gf_EX(static_grn, M0=1e24, ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_ex.png")
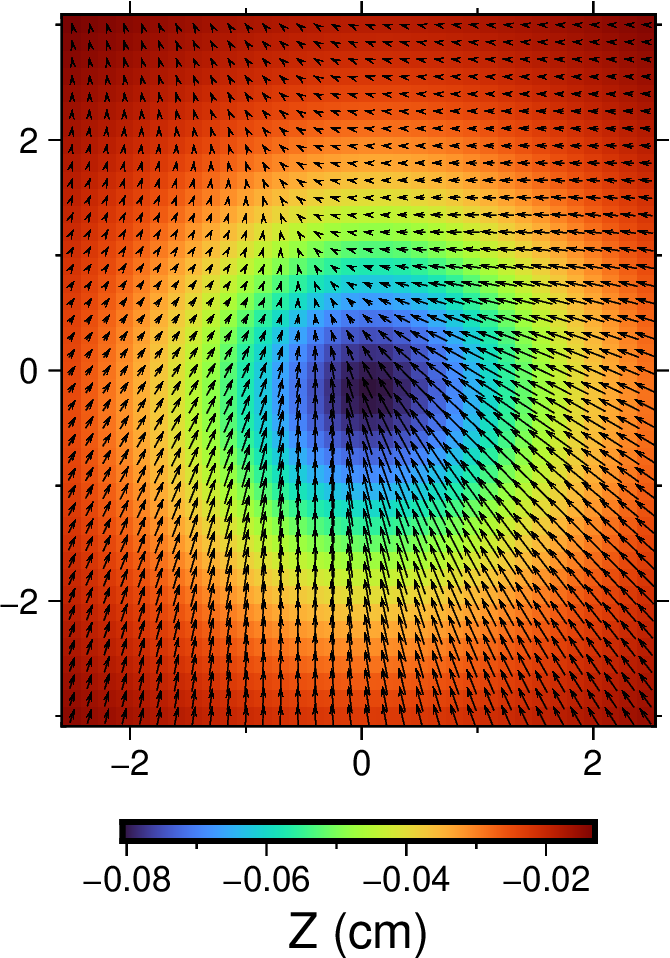
单力源
北向力 \(f_N=1\),东向力 \(f_E=-0.5\),垂直向下的力 \(f_Z=2\),单位 1e16 dyne。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e16 -F1/-0.5/2 -N -Gstgrn.nc -Ostsyn_sf.nc
static_syn = pygrt.utils.gen_syn_from_gf_SF(static_grn, S=1e16, fN=1, fE=-0.5, fZ=2, ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_sf.png")
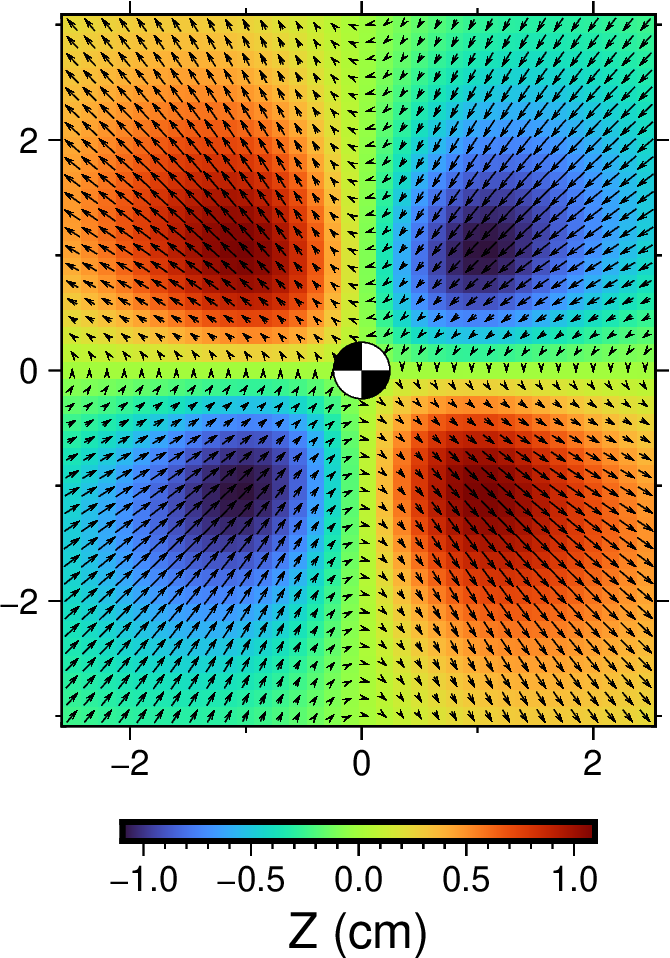
剪切源
断层走向33°,倾角50°,滑动角120°,标量矩 1e24 dyne·cm。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e24 -M33/50/120 -N -Gstgrn.nc -Ostsyn_dc.nc
static_syn = pygrt.utils.gen_syn_from_gf_DC(static_grn, M0=1e24, strike=33, dip=50, rake=120, ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_dc.png")
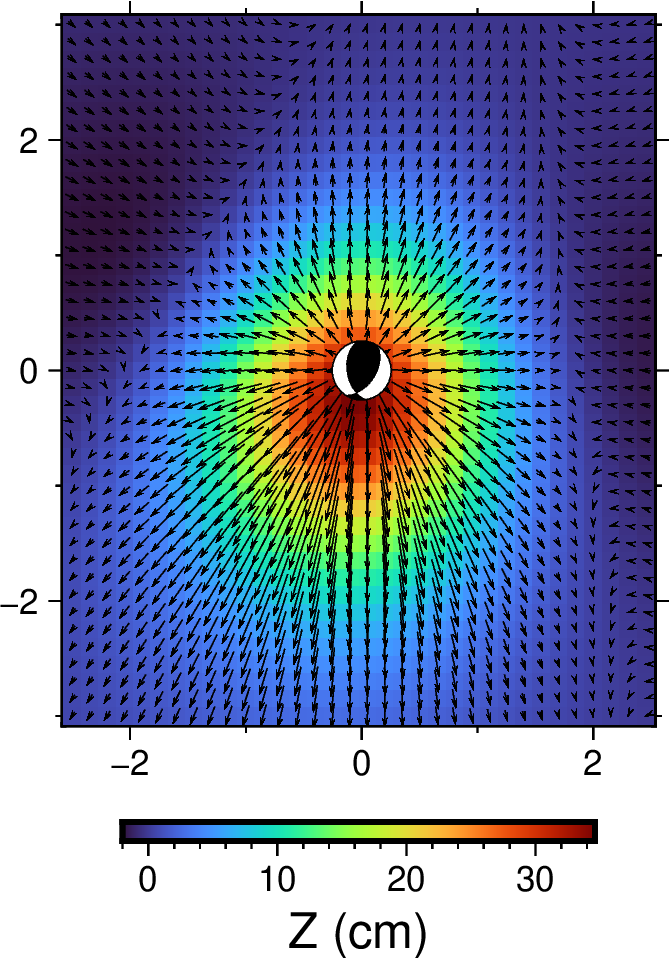
这里如果改变倾角为90°,滑动角0°,就可以看到清晰的蝴蝶状辐射花样。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e24 -M33/90/0 -N -Gstgrn.nc -Ostsyn_dc2.nc
static_syn = pygrt.utils.gen_syn_from_gf_DC(static_grn, M0=1e24, strike=33, dip=90, rake=0, ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_dc2.png")
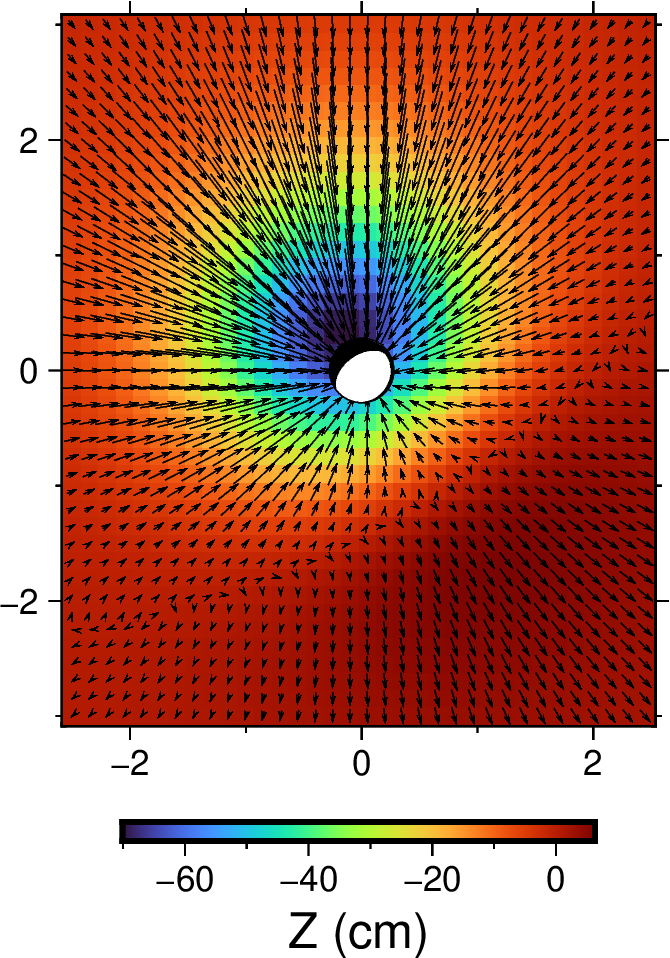
矩张量源
\(M_{xx}=0.1, M_{xy}=-0.2, M_{xz}=1.0, M_{yy}=0.3, M_{yz}=-0.5, M_{zz}=-2.0\),单位 1e24 dyne·cm, 其中X为北向,Y为东向,Z为垂直向下。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e24 -T0.1/-0.2/1.0/0.3/-0.5/-2.0 -N -Gstgrn.nc -Ostsyn_mt.nc
static_syn = pygrt.utils.gen_syn_from_gf_MT(static_grn, M0=1e24, MT=[0.1,-0.2,1.0,0.3,-0.5,-2.0], ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_mt.png")
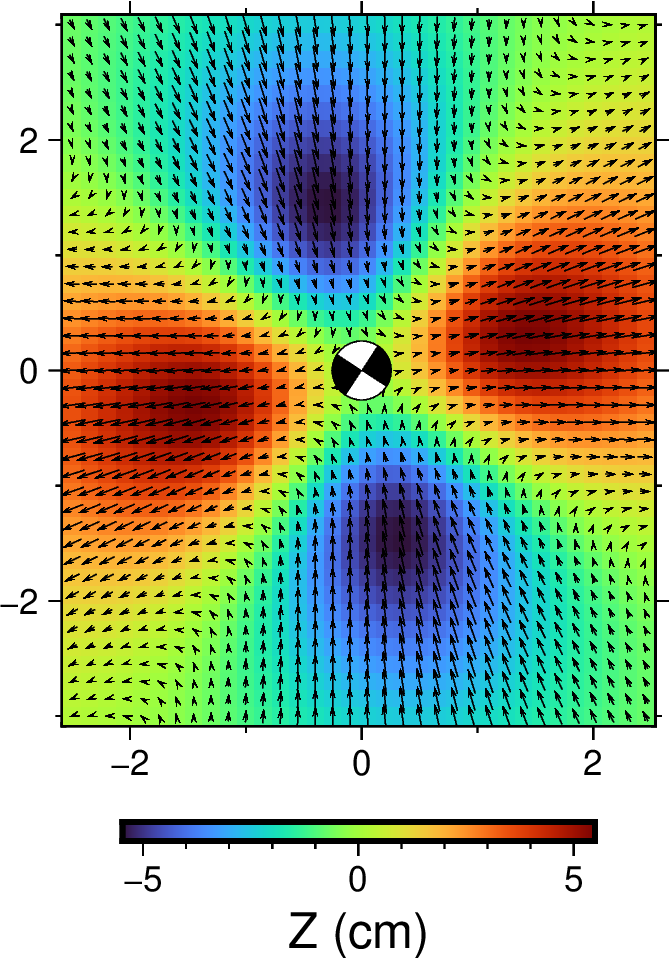
若指定 \(M_{xy}=-0.2\),其它均为零,则为纯剪切。
# 从网格文件中读取格林函数,再将合成结果写入新网格
grt static syn -S1e24 -T0/-0.2/0/0/0/0 -N -Gstgrn.nc -Ostsyn_mt2.nc
static_syn = pygrt.utils.gen_syn_from_gf_MT(static_grn, M0=1e24, MT=[0,-0.2,0,0,0,0], ZNE=True)
print(static_syn.keys())
# dict_keys(['_xarr', '_yarr', '_src_va', '_src_vb', '_src_rho', '_rcv_va', '_rcv_vb', '_rcv_rho', 'Z', 'N', 'E'])
plot_static(static_syn, "syn_mt2.png")